摘要:8.已知方程的四个根组成一个首项为的等差数列.则|m-n|= A.1 [分析] 本题主要考查二次方程根与系数的关系.等差数列等基本知识.以及数学思维和分析处理问题的能力. 注意到题设4次方程的两个2次因式中.只有常数项不同.可知等差数列的4个项中首尾两项应为其中一个因式的两根.而中间两项为另一因式的两根.所以.在此基础上.可用不同的引入方式.采取适当的计算程序.求得|m-n|的值. 解法1 因为抛物线有公共的对称轴x=1.又它们与x轴的4个交点的横坐标成等差数列.所以可设为 的一个根.则方程的另一个根为 解法3 依题意可设原方程的4个根为 则对任意实数x.有 比较系数.得 (注:m.n的位置也可对调.不影响结果). 解法4 从解原方程入手.由 求得原方程的根为: 由题设.这4个根组成首项为的等差数列.所以.必有1-m>0.1-n>0.且 [答案] C
网址:http://m.1010jiajiao.com/timu3_id_501244[举报]
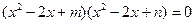 的四个根组成一个首项为
的四个根组成一个首项为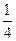 的等差数列,
的等差数列,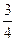 C.
C.
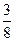
 的四个根组成一个首项为
的四个根组成一个首项为 的等比数列,则
的等比数列,则


