摘要：18．∵四边形AA1C1C是菱形.∠C1CA=60°.∴△AC1A1是正三角形.又P是A1C1 的中点.∴PA⊥A1C1.--2分 ∴PA⊥AC. 又PA⊥BC.AC∩BC=C ∴PA⊥平面ABC.--4分 .PA⊥平面ABC.∴PA⊥平面 A1B1C1.由△AC1A1是正三角形.∴PB1⊥A1C1. 6分 ∴B1P⊥平面AA1C1C.∴B1P⊥CC1. ∴CC1与B1P所成的角的正弦值为1.----8分 (3)--10分 -----12分
网址：http://m.1010jiajiao.com/timu3_id_501093[举报]
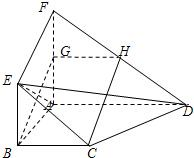如图，面ABEF⊥面ABCD，四边形ABEF与四边形ABCD都是直角梯形，∠BAD=∠FAB=90°，BC
| ||
. |
| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
（Ⅰ）证明：四边形BCHG是平行四边形；
（Ⅱ）C、D、E、F四点是否共面？为什么？ 查看习题详情和答案>>
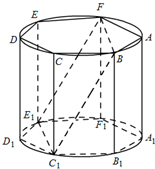（2012•肇庆二模）如图，ABCDEF-A1B1C1D1E1F1是底面半径为1的圆柱的内接正六棱柱（底面是正六边形，侧棱垂直于底面），过FB作圆柱的截面交下底面于C1E1，已知FC1=| 13 |
（1）证明：四边形BFE1C1是平行四边形；
（2）证明：FB⊥CB1；
（3）求三棱锥A-A1BF的体积．
（2009•普宁市模拟）如图抛物线x2=2py的焦点为F，准线为l，过抛物线上一点P（不过原点），做抛物线的切线分别交x轴、y轴于A、B两点．（Ⅰ）求证：|PA|=|AB|；
（Ⅱ）若过F、A的直线交准线l于C，证明：四边形PFBC为菱形．
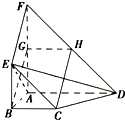如图，平面ABEF⊥平面ABCD，四边形ABEF与ABCD都是直角梯形，∠BAD=∠FAB=90°，BC