摘要：解析: P在直线OC上.可设P(2x,x), ∴·=(1-2x)×(5-2x)+(7-x)×(1-x)=5(x-2)2-8, ·最小时P(4,2). ∴cos∠APB==-,∠APB=arccos(-). 答案: A
网址：http://m.1010jiajiao.com/timu3_id_500768[举报]
在平面直角坐标系xOy中，已知点A（-1，-2），B（2，3），C（-2，-1）．
（1）求以线段AB，AC为邻边的平行四边形的两条对角线的长；
（2）在直线OC上是否存在一点P，使(
-
)•
=0？若存在求出P点坐标，若不存在请说明理由．
查看习题详情和答案>>
（1）求以线段AB，AC为邻边的平行四边形的两条对角线的长；
（2）在直线OC上是否存在一点P，使(
| AB |
| OP |
| OC |
已知平面坐标系中，点O为原点，A（-3，-4），B（5，-12）
（1）若
=
+
，
=
-
，求
及
的坐标；
（2）求
•
；
（3）若点P在直线AB上，且
⊥
，求
的坐标．
查看习题详情和答案>>
（1）若
| OC |
| OA |
| OB |
| OD |
| OA |
| OB |
| OC |
| OD |
（2）求
| OA |
| OB |
（3）若点P在直线AB上，且
| OP |
| AB |
| OP |
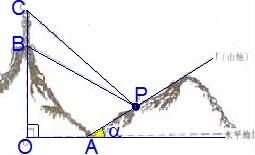某人在一山坡P处观看对面山项上的一座铁塔，如图所示，塔及所在的山崖可视为图中的竖线OC，塔高BC?80（米），山高OB?220（米），OA?200（米），图中所示的山坡可视为直线l且点P在直线l上，l与水平地面的夹角为α，tanα=| 1 | 2 |
．试问，此人距山崖的水平地面多高时，观看塔的视角∠BPC最大（不计此人的身高）？
．试问，此人距山崖的水平地面多高时，观看塔的视角∠BPC最大（不计此人的身高）？