题目内容

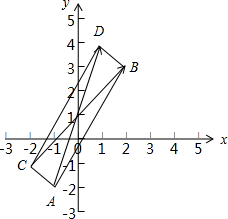
在平面直角坐标系xOy中，已知点A（-1，-2），B（2，3），C（-2，-1）．
（1）求以线段AB，AC为邻边的平行四边形的两条对角线的长；
（2）在直线OC上是否存在一点P，使(
AB
-
OP
)•
OC
=0？若存在求出P点坐标，若不存在请说明理由．
分析：（1）以线段AB，AC为邻边的平行四边形的两条对角线对应的向量为
AB
+
AC
和
AB
-
AC
，求出坐标后，代入向量模的计算公式，可得答案．
（2）由
OC
=（-2，-1），P点在直线OC上，故可设
OP
=（2t，t），进而根据(
AB
-
OP
)•
OC
=0，可得t值，进而得到P点坐标．
解答：解：（1）∵点A（-1，-2），B（2，3），C（-2，-1）．
∴
AB
=（3，5），
AC
=（-1，1）

∵
AD
=
AB
+
AC
=（2，6），
CB
=
AB
-
AC
=（4，4）
|
AD
|=
22+62
=2
10
，|
CB
|=
42+42
=4
2

即以线段AB，AC为邻边的平行四边形的两条对角线的长分别为4
2
，2
10

（2）存在P(
22
5
，
11
5
)满足条件，理由如下：
∵
OC
=（-2，-1），故可设
OP
=（2t，t）
则
AB
-
OP
=（3-2t，5-t）
(
AB
-
OP
)•
OC
=（3-2t）×（-2）+（5-t）×（-1）=5t-11=0
解得t=
11
5

故P点坐标为P(
22
5
，
11
5
)
点评：本题考查的知识点是平面向量加法的平行四边形法则，平面向量的模，平面向量数量积运算，是平面向量的综合应用，难度不大，属于基础题．
练习册系列答案
相关题目
在平面直角坐标系xoy中，已知圆心在直线y=x+4上，半径为2
2
的圆C经过坐标原点O，椭圆
x2
a2
+
y2
9
=1(a＞0)与圆C的一个交点到椭圆两焦点的距离之和为10．
（1）求圆C的方程；
（2）若F为椭圆的右焦点，点P在圆C上，且满足PF=4，求点P的坐标．
如图，在平面直角坐标系xOy中，锐角α和钝角β的终边分别与单位圆交于A，B两点．若点A的横坐标是
3
5
，点B的纵坐标是
12
13
，则sin（α+β）的值是
16
65
16
65
．
在平面直角坐标系xOy中，若焦点在x轴的椭圆
x2
m
+
y2
3
=1的离心率为
1
2
，则m的值为
4
4
．
（2013•泰州三模）选修4-4：坐标系与参数方程
在平面直角坐标系xOy中，已知A（0，1），B（0，-1），C（t，0），D(
3t
，0)，其中t≠0．设直线AC与BD的交点为P，求动点P的轨迹的参数方程（以t为参数）及普通方程．
（2013•东莞一模）在平面直角坐标系xOy中，已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左焦点为F1（-1，0），且椭圆C的离心率e=
1
2
．
（1）求椭圆C的方程；
（2）设椭圆C的上下顶点分别为A1，A2，Q是椭圆C上异于A1，A2的任一点，直线QA1，QA2分别交x轴于点S，T，证明：|OS|•|OT|为定值，并求出该定值；
（3）在椭圆C上，是否存在点M（m，n），使得直线l：mx+ny=2与圆O：x2+y2=
16
7
相交于不同的两点A、B，且△OAB的面积最大？若存在，求出点M的坐标及对应的△OAB的面积；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网