摘要:设全集U=R. (1)解关于x的不等式|x-1|+a-1>0(a∈R), (2)记A为(1)中不等式的解集.集合B={x|sin(πx-)+cos(πx-)=0}. 若(UA)∩B恰有3个元素.求a的取值范围. 解:(1)由|x-1|+a-1>0.得|x-1|>1-a. 当a>1时.解集是R, 当a≤1时.解集是{x|x<a或x>2-a}. (2)当a>1时.UA=, 当a≤1时.UA={x|a≤x≤2-a}. 因sin(πx-)+cos(πx-)=2[sin(πx-)cos+cos(πx-)sin]=2sinπx. 由sinπx=0.得πx=kπ(k∈Z).即x=k∈Z.所以B=Z. 当(UA)∩B恰有3个元素时.a应满足 解得-1<a≤0.
网址:http://m.1010jiajiao.com/timu3_id_500614[举报]
设全集U=R,关于x的不等式|x+2|+a-2>0(a∈R)的解集为A.
(1)分别求出当a=1和a=3时的集合A;
(2)设集合B={x|
sin(πx-
)+cos(πx-
)=0},若(CUA)∩B中有且只有三个元素,求实数a的取值范围.
查看习题详情和答案>>
(1)分别求出当a=1和a=3时的集合A;
(2)设集合B={x|
| 3 |
| π |
| 6 |
| π |
| 6 |
设全集U=R,关于x的不等式|x+2|+a-2>0(a∈R)的解集为A.
(1)分别求出当a=1和a=3时的集合A;
(2)设集合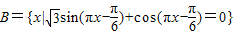 ,若(CUA)∩B中有且只有三个元素,求实数a的取值范围.
,若(CUA)∩B中有且只有三个元素,求实数a的取值范围.
查看习题详情和答案>>
(1)分别求出当a=1和a=3时的集合A;
(2)设集合
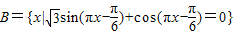 ,若(CUA)∩B中有且只有三个元素,求实数a的取值范围.
,若(CUA)∩B中有且只有三个元素,求实数a的取值范围.查看习题详情和答案>>
设全集U=R,关于x的不等式|x+2|+a-2>0(a∈R)的解集为A.
(1)分别求出当a=1和a=3时的集合A;
(2)设集合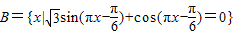 ,若(CUA)∩B中有且只有三个元素,求实数a的取值范围.
,若(CUA)∩B中有且只有三个元素,求实数a的取值范围.
查看习题详情和答案>>
(1)分别求出当a=1和a=3时的集合A;
(2)设集合
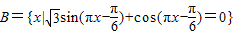 ,若(CUA)∩B中有且只有三个元素,求实数a的取值范围.
,若(CUA)∩B中有且只有三个元素,求实数a的取值范围.查看习题详情和答案>>
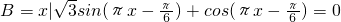 ,若(CUA)∩B中有且只有三个元素,求实数a的取值范围.
,若(CUA)∩B中有且只有三个元素,求实数a的取值范围.