题目内容
设全集U=R,关于x的不等式|x+2|+a-2>0(a∈R)的解集为A.
(1)分别求出当a=1和a=3时的集合A;
(2)设集合B={x|
sin(πx-
)+cos(πx-
)=0},若(CUA)∩B中有且只有三个元素,求实数a的取值范围.
(1)分别求出当a=1和a=3时的集合A;
(2)设集合B={x|
| 3 |
| π |
| 6 |
| π |
| 6 |
分析:(1)根据所给的a的值,代入不等式,根据绝对值不等式的意义,写出不等式的解集,当a=1时,A=(-∞,-3)∪(-1,+∞),当a=3时,A=R.
(2)由|x+2|+a-2>0可以得到:|x+2|>2-a,当a>2,解集是R,根据a的取值不同,写出对应的补集,根据集合的交并运算求出结果.
(2)由|x+2|+a-2>0可以得到:|x+2|>2-a,当a>2,解集是R,根据a的取值不同,写出对应的补集,根据集合的交并运算求出结果.
解答:解:(1)当a=1时,A=(-∞,-3)∪(-1,+∞)…(3分)
当a=3时,A=R…(6分)
(2)由|x+2|+a-2>0可以得到:|x+2|>2-a.
当a>2,解集是R;
当a≤2时,解集是{x|x<a-4或x>-a}…(8分)
(i)当a>2时,CUA=φ,不合题意;
(ii)当a≤2时,CUA={x|a-4≤x≤-a}…(10分)
因
sin(πx-
)+cos(πx-
)=2[sin(πx-
)cos
+cos(πx-
)sin
]
=2sinπx
由sinπx=0,得πx=kπ(k∈Z),即x=k∈Z,所以B=Z…(12分)
当(CUA)∩B有3个元素时,a就满足
可以得到:0<a≤1…(14分)
当a=3时,A=R…(6分)
(2)由|x+2|+a-2>0可以得到:|x+2|>2-a.
当a>2,解集是R;
当a≤2时,解集是{x|x<a-4或x>-a}…(8分)
(i)当a>2时,CUA=φ,不合题意;
(ii)当a≤2时,CUA={x|a-4≤x≤-a}…(10分)
因
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
=2sinπx
由sinπx=0,得πx=kπ(k∈Z),即x=k∈Z,所以B=Z…(12分)
当(CUA)∩B有3个元素时,a就满足
|
可以得到:0<a≤1…(14分)
点评:本题考查集合的运算和不等式的解集的求法,本题解题的关键是求出不等式的解集和熟练应用集合之间的关系,本题是一个中档题目.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
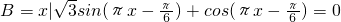 ,若(CUA)∩B中有且只有三个元素,求实数a的取值范围.
,若(CUA)∩B中有且只有三个元素,求实数a的取值范围.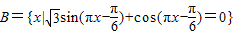 ,若(CUA)∩B中有且只有三个元素,求实数a的取值范围.
,若(CUA)∩B中有且只有三个元素,求实数a的取值范围.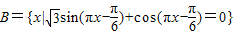 ,若(CUA)∩B中有且只有三个元素,求实数a的取值范围.
,若(CUA)∩B中有且只有三个元素,求实数a的取值范围.