摘要：(1+x)2n+x(1+x)2n-1+x2(1+x)2n-2+······+xn(1+x)n的展开式中.含xn项的系数为劲( ) (A) (B) (C) (D)
网址：http://m.1010jiajiao.com/timu3_id_500468[举报]
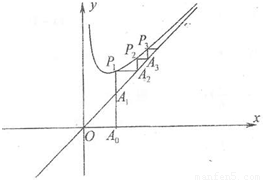
函数f（x）=x+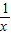
，g（x）=x，已知A（x，0），（x＞0），如图，过A作平行于y轴的直线交y=g（x）的图象于A1，交y=f（x）的图象于P1，要过P1作平行于x轴的直线交y=g（x）于A2，再过A2作平行于y轴的直线交y=f（x）于P2，…，这样一直作下去；设△A1P1A2的面积为S1，…，△AkPkAk+1的面积为Sk，数列{Sn}的前n项和为Tn，并设Pn（xn，yn）．
（1）求S1，S2；
（2）求证：yn2=2Tn+2n+x2；
（3）若x=5，求证：45＜y1000＜45.1．
查看习题详情和答案>>
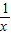，g（x）=x，已知A（x，0），（x＞0），如图，过A作平行于y轴的直线交y=g（x）的图象于A1，交y=f（x）的图象于P1，要过P1作平行于x轴的直线交y=g（x）于A2，再过A2作平行于y轴的直线交y=f（x）于P2，…，这样一直作下去；设△A1P1A2的面积为S1，…，△AkPkAk+1的面积为Sk，数列{Sn}的前n项和为Tn，并设Pn（xn，yn）．（1）求S1，S2；
（2）求证：yn2=2Tn+2n+x2；
（3）若x=5，求证：45＜y1000＜45.1．
查看习题详情和答案>>
已知函数f(x)=x2-(-1)K·2lnx(k∈N*).
（1）讨论函数f(x)的单调性；
（2）k是偶数时，正项数列{an}满足a1=1,f′(an)=
，求{an}的通项公式；
（3）k是奇数，x＞0，n∈N*时，求证：［f′(x)］n-2n-1·f′(xn)≥2n(2n-2).
查看习题详情和答案>>
已知f（x）在（-1，1）上有定义，f（
）=-1，且满足x，y∈（-1，1）有f（x）+f（y）=f（
）
（1）证明：f（x）在（-1，1）上为奇函数；?
（2）对数列x1=
，xn+1=
，求f（xn）；?
（3）求证
+
+…+
＞-
查看习题详情和答案>>
| 1 |
| 2 |
| x+y |
| 1+xy |
（1）证明：f（x）在（-1，1）上为奇函数；?
（2）对数列x1=
| 1 |
| 2 |
| 2xn |
| 1+xn2 |
（3）求证
| 1 |
| f(x1) |
| 1 |
| f(x2) |
| 1 |
| f(xn) |
| 2n+5 |
| n+2 |