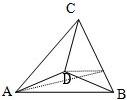
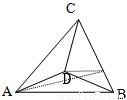
摘要：解:⑴设E(x.y).D(x0.y0) ∵ABCD是平行四边形.∴. ∴(4.0)+(x0+2.y0)=2∴(x0+6.y0)= ∴ 又 即: ∴□ABCD对角线交点E的轨迹方程为 ⑵设过A的直线方程为 以A.B为焦点的椭圆的焦距2C=4.则C=2 设椭圆方程为 . 即-------(*) 将代入(*)得 即 设M(x1.y1).N(x2.y2)则 ∵MN中点到Y轴的距离为.且MN过点A.而点A在Y轴的左侧.∴MN中点也在Y轴的左侧. ∴.∴ ∴ ∵ ∴ ∴ 即 ∴ ∴ ∴ . .∵ .∴ ∴ ∴所求椭圆方程为 ⑶由⑴可知点E的轨迹是圆 设是圆上的任一点.则过点的切线方程是 ①当时.代入椭圆方程得: .又 ∴ ∴ = 令 则 . ∵ ∴当t=15时. 取最大值为15 .的最大值为. 此时 .∴直线l的方程为 ②当时.容易求得 故:所求的最大值为.此时l的方程为
网址：http://m.1010jiajiao.com/timu3_id_500048[举报]
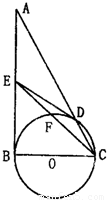
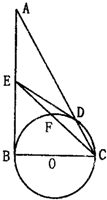（选修4-1）如图，在△ABC中，∠ABC=90°，以BC为直径的圆O交AC于点D，设E为AB的中点． （I）求证：直线DE为圆O的切线；
（Ⅱ）设CE交圆O于点F，求证：CD•CA=CF•CE
（选修4-4）在平面直角坐标系xoy中，圆C的参数方程为
|
| π |
| 3 |
（I）写出圆C的标准方程和直线l的参数方程；
（Ⅱ）设直线l与圆C相交于A，B两点，求|PA|-|PB|的值．
（选修4-5）已知函数f（x）=|2x+1|，g（x）=|x|+a
（Ⅰ）当a=0时，解不等式f（x）≥g（x）；
（Ⅱ）若存在x∈R，使得f（x）≤g（x）成立，求实数a的取值范围．
（选修4-1）如图，在△ABC中，∠ABC=90°，以BC为直径的圆O交AC于点D，设E为AB的中点．
（I）求证：直线DE为圆O的切线；
（Ⅱ）设CE交圆O于点F，求证：CD•CA=CF•CE
（选修4-4）在平面直角坐标系xoy中，圆C的参数方程为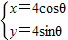
（θ为参数），直线l经过点p（2，2），倾斜角a=
．
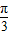（I）写出圆C的标准方程和直线l的参数方程；
（Ⅱ）设直线l与圆C相交于A，B两点，求|PA|-|PB|的值．
（选修4-5）已知函数f（x）=|2x+1|，g（x）=|x|+a
（Ⅰ）当a=0时，解不等式f（x）≥g（x）；
（Ⅱ）若存在x∈R，使得f（x）≤g（x）成立，求实数a的取值范围．
查看习题详情和答案>>
（I）求证：直线DE为圆O的切线；
（Ⅱ）设CE交圆O于点F，求证：CD•CA=CF•CE
（选修4-4）在平面直角坐标系xoy中，圆C的参数方程为
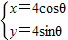（θ为参数），直线l经过点p（2，2），倾斜角a=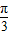．（I）写出圆C的标准方程和直线l的参数方程；
（Ⅱ）设直线l与圆C相交于A，B两点，求|PA|-|PB|的值．
（选修4-5）已知函数f（x）=|2x+1|，g（x）=|x|+a
（Ⅰ）当a=0时，解不等式f（x）≥g（x）；
（Ⅱ）若存在x∈R，使得f（x）≤g（x）成立，求实数a的取值范围．
查看习题详情和答案>>