摘要：(1)f1(0)=2,a1==,fn+1(0)=f1［fn(0)］=, an+1====-=-an, 4分 ∴数列{an}是首项为,公比为-的等比数列.∴an=(-)n-1. 6分 (2)T2n=a1+2a2+3a3+-+(2n-1)a2n-1+2na2n, -T2n=(-a1)+(-)2a2+(-)3a3+-+(-)(2n-1)a2n-1+(-)·2na2n =a2+2a3+-+(2n-1)a2n-na2n, 8分 两式相减得T2n=a1+a2+a3+-+a2n+na2n, 所以.T2n=+n×(-)2n-1=-(-)2n+(-)2n-1, 10分 T2n=-(-)2n+(-)2n-1=(1-). ∴9T2n=1-, Qn=1-, 12分 当n=1时.22n=4,(2n+1)2=9,∴9T2n＜Qn; 当n=2时.22n=16,(2n+1)2=25,∴9T2n＜Qn; 13分 当n≥3时.22n=［(1+1)n］2 =(C+C+C+-+C)2＞(2n+1)2,∴9T2n＞Qn. 14分
网址：http://m.1010jiajiao.com/timu3_id_500038[举报]
设a1，a2，…，an为1，2，…，n按任意顺序做成的一个排列，fk是集合{ai|ai＜ak，i＞k}元素的个数，而gk是集合{ai|ai＞ak，i＜k}元素的个数（k=1，2，…，n），规定fn=g1=0，例如：对于排列3，1，2，f1=2，f2=0，f3=0
（I）对于排列4，2，5，1，3，求
fk
（II）对于项数为2n-1 的一个排列，若要求2n-1为该排列的中间项，试求
gk的最大值，并写出相应得一个排列
（Ⅲ）证明
fk=
gk．
查看习题详情和答案>>
（I）对于排列4，2，5，1，3，求
| n |
 |
| k=1 |
（II）对于项数为2n-1 的一个排列，若要求2n-1为该排列的中间项，试求
| n |
|
| k=1 |
（Ⅲ）证明
| n |
|
| k=1 |
| n |
|
| k=1 |
设a1，a2，…，an为1，2，…，n按任意顺序做成的一个排列，fk是集合{ai|ai＜ak，i＞k}元素的个数，而gk是集合{ai|ai＞ak，i＜k}元素的个数（k=1，2，…，n），规定fn=g1=0，例如：对于排列3，1，2，f1=2，f2=0，f3=0
（I）对于排列4，2，5，1，3，求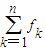
（II）对于项数为2n-1 的一个排列，若要求2n-1为该排列的中间项，试求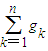
的最大值，并写出相应得一个排列
（Ⅲ）证明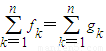
．
查看习题详情和答案>>
（I）对于排列4，2，5，1，3，求
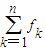
（II）对于项数为2n-1 的一个排列，若要求2n-1为该排列的中间项，试求
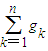的最大值，并写出相应得一个排列（Ⅲ）证明
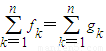．查看习题详情和答案>>
已知f0(x)=xex，f1(x)=f0′(x)，f2(x)=f1′(x)，…fn(x)=fn-1′(x)，n∈N*
（1）请写出fn（x）的表达式（不需要证明）；
（2）求fn（x）的极小值；
（3）设gn(x)=-x2-2(n+1)x-8n+8，gn（x）的最大值为a，fn（x）的最小值为b，证明：a-b≥e-4．
查看习题详情和答案>>
（1）请写出fn（x）的表达式（不需要证明）；
（2）求fn（x）的极小值；
（3）设gn(x)=-x2-2(n+1)x-8n+8，gn（x）的最大值为a，fn（x）的最小值为b，证明：a-b≥e-4．