摘要:(1)设点M的坐标为(x,y).由=-,得P(0,-),Q(,0), 2分 由·=0.得(3.-)(x,)=0,又得y2=4x, 5分 由点Q在x轴的正半轴上.得x>0, 所以.动点M的轨迹C是以为焦点的抛物线.除去原点. 6分 (2)设直线l:y=k(x+1),其中k≠0,代入y2=4x,得k2x2+2(k2-2)x+k2=0,① 7分 设A(x1,y1),B(x2,y2), 则x1,x2是方程①的两个实根.∴x1+x2=-,x1x2=1, 所以.线段AB的中点坐标为(,), 8分 线段AB的垂直平分线方程为y-=-(x-), 9分 令y=0,x0=+1,所以点E的坐标为(+1,0) 因为△ABE为正三角形.所以点E(+1,0)到直线AB的距离等于|AB|, 而|AB|==·, 10分 所以.=, 11分 解得k=±,得x0=. 12分
网址:http://m.1010jiajiao.com/timu3_id_500037[举报]
在平面直角坐标系中,圆M∶(x-1)2+(y-1)2=5在点A(3,2)处的切线方程可如下求解:设P(x,y)为切线上任一点,则由向量方法可得切线方程为:2x+y-8=0,类似地,在空间直角坐标系中,球M∶(x-1)2+(y-1)2+(z-1)2=6在点A(3,2,2)处的切面方程为________.
设不等边三角形ABC的外心与重心分别为M、G,若A(-1,0),B(1,0)且MG//AB.
(Ⅰ)求三角形ABC顶点C的轨迹方程;
(Ⅱ)设顶点C的轨迹为D,已知直线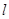 过点(0,1)并且与曲线D交于P、N两点,若O为坐标原点,满足OP⊥ON,求直线
过点(0,1)并且与曲线D交于P、N两点,若O为坐标原点,满足OP⊥ON,求直线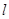 的方程.
的方程.
【解析】
第一问因为设C(x,y)(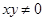 )
)
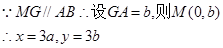 ……3分
……3分
∵M是不等边三解形ABC的外心,∴|MA|=|MC|,即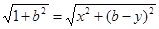 (2)
(2)
由(1)(2)得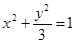 .所以三角形顶点C的轨迹方程为
.所以三角形顶点C的轨迹方程为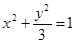 ,
,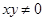 .…6分
.…6分
第二问直线l的方程为y=kx+1
由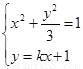 消y得
消y得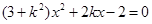 。 ∵直线l与曲线D交于P、N两点,∴△=
。 ∵直线l与曲线D交于P、N两点,∴△=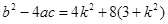 ,
,
又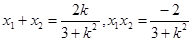 ,
,
∵ ,∴
,∴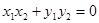
 得到直线方程。
得到直线方程。
查看习题详情和答案>>
 (Ⅲ)给出定点M(0,2),设P、Q分别为直线l和圆O上动点,求|MP|+|PQ|的最小值及此时点P的坐标.
(Ⅲ)给出定点M(0,2),设P、Q分别为直线l和圆O上动点,求|MP|+|PQ|的最小值及此时点P的坐标.