摘要：以椭圆＝1(a＞1)短轴一端点为直角顶点.作椭圆内接等腰直角三角形.试判断并推证能作出多少个符合条件的三角形. 5 已知.二次函数f(x)＝ax2+bx+c及一次函数g(x)＝-bx.其中a.b.c∈R.a＞b＞c.a+b+c＝0. (Ⅰ)求证:f(x)及g(x)两函数图象相交于相异两点, (Ⅱ)设f(x).g(x)两图象交于A.B两点.当AB线段在x轴上射影为A1B1时.试求|A1B1|的取值范围. 6 已知过函数f(x)=的图象上一点B(1.b)的切线的斜率为-3. (1) 求a.b的值, (2) 求A的取值范围.使不等式f(x)≤A-1987对于x∈[-1.4]恒成立, (3) 令.是否存在一个实数t.使得当时.g(x)有最大值1? 7 已知两点M.动点P在y轴上的射影为H.︱︱是2和的等比中项. (1) 求动点P的轨迹方程.并指出方程所表示的曲线, (2) 若以点M.N为焦点的双曲线C过直线x+y=1上的点Q.求实轴最长的双曲线C的方程.
网址：http://m.1010jiajiao.com/timu3_id_500006[举报]
已知椭圆
＝1(a＞b＞0)的离心率为
，短轴的一个端点为M(0，1)，直线l：y＝kx－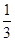
与椭圆相交于不同的两点A、B.
(1)若AB＝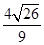
，求k的值；
(2)求证：不论k取何值，以AB为直径的圆恒过点M.
已知椭圆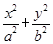
＝1(a＞b＞0)的离心率为
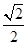，短轴的一个端点为M(0，1)，直线l：y＝kx－
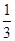与椭圆相交于不同的两点A、B.
(1)若AB＝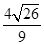
，求k的值；
(2)求证：不论k取何值，以AB为直径的圆恒过点M.
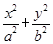＝1(a＞b＞0)的离心率为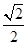，短轴的一个端点为M(0，1)，直线l：y＝kx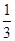－与椭圆相交于不同的两点A、B.(1)若AB＝
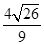，求k的值；(2)求证：不论k取何值，以AB为直径的圆恒过点M.
已知椭圆
＋
＝1(a＞b＞0)的两焦点与短轴的一个端点的连线构成等腰直角三角形，直线x－y＋b＝0是抛物线y2＝4x的一条切线．
(Ⅰ)求椭圆的方程；
(Ⅱ)过点S(0，－
)的动直线L交椭圆C于A、B两点．问：是否存在一个定点T，使得以AB为直径的圆恒过点T？若存在，求点T坐标；若不存在，说明理由．
＋
＝1(a＞b＞0)的两焦点与短轴的一个端点的连线构成等腰直角三角形，直线x－y＋b＝0是抛物线y2＝4x的一条切线．
)的动直线L交椭圆C于A、B两点．问：是否存在一个定点T，使得以AB为直径的圆恒过点T？若存在，求点T坐标；若不存在，说明理由．
＋
＝1(a＞b＞0)经过点P(1，
)，且两焦点与短轴的一个端点的连线构成等腰直角三角形．
n＝0(m，n∈R)交椭圆C于A、B两点，试问：在坐标平面上是否存在一个定点T，使得以AB为直径的圆恒过点T．若存在，求出点T的坐标；若不存在，请说明理由．