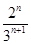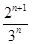摘要：已知数列{an}满足a1＝2.对于任意的n∈N.都有an＞0. 且(n+1)a+anan+1-na＝0.又知数列{bn}:b1＝2n-1+1 (1)求数列{an}的通项an以及它的前n项和Sn, (2)求数列{bn}的前n项和Tn, (3)猜想Sn和Tn的大小关系.并说明理由. 解:(Ⅰ)∵ ∴. ∴ ∴.∴. 即. ∴. ∴.∴又.∴. ∴ . (Ⅱ)∵. ∴ . (Ⅲ) 当时..∴, 当时..∴, 当时..∴, 当时..∴, 当时..∴, 当时..∴. 猜想:当时.. 即.亦即. 下面用数学归纳法证明: 当时.前面已验证成立, 假设时.成立.那么当时. . ∴当时.也成立. 由以上.可知.当时.有,当时., 当时..
网址：http://m.1010jiajiao.com/timu3_id_499368[举报]
已知数列{an}满足a1＝2，对于任意的n∈N，都有an＞0，且(n＋1)a
＋anan＋1－na
＝0，又知数列{bn}:b1＝2n－1＋1
(1)求数列{an}的通项an以及它的前n项和Sn；
(2)求数列{bn}的前n项和Tn；
(3)猜想Sn和Tn的大小关系，并说明理由.
查看习题详情和答案>>已知数列{an}满足a1＝2，对于任意的n∈N，都有an＞0，且(n＋1)a
＋anan＋1－na
＝0，又知数列{bn}:b1＝2n－1＋1
(1)求数列{an}的通项an以及它的前n项和Sn；
(2)求数列{bn}的前n项和Tn；
(3)猜想Sn和Tn的大小关系，并说明理由.
＋anan＋1－na＝0，又知数列{bn}:b1＝2n－1＋1(1)求数列{an}的通项an以及它的前n项和Sn；
(2)求数列{bn}的前n项和Tn；
(3)猜想Sn和Tn的大小关系，并说明理由.
＋anan+1＋
＝0，又知数列{bn} bn＝2n－1＋1
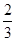，且对任意的正整数m，n，都有am＋n＝am·an，若数列{an}的前n项和为Sn，则Sn等于( )
．
；
时，是否存在正整数m，使得对于任意正整数n都有bn≥bm？如果存在，求出m的值；如果不存在，请说明理由．