摘要:22.数列 (1)若数列 (2)求数列的通项公式 (3)数列适合条件的项,若不存在.请说明理由
网址:http://m.1010jiajiao.com/timu3_id_499328[举报]
(本题满分14分)设直线![]() . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有![]() . 则称直线l为曲线S的“上夹线”.(Ⅰ)已知函数
. 则称直线l为曲线S的“上夹线”.(Ⅰ)已知函数![]() .求证:
.求证:![]() 为曲线
为曲线![]() 的“上夹线”.
的“上夹线”.
(Ⅱ)观察下图:
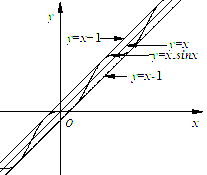

根据上图,试推测曲线![]() 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.
(本题满分14分)已知![]() 是给定的实常数,设函数
是给定的实常数,设函数![]() ,
,![]() ,
,
![]() 是
是![]() 的一个极大值点.
的一个极大值点.
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)设![]() 是
是![]() 的3个极值点,问是否存在实数
的3个极值点,问是否存在实数![]() ,可找到
,可找到![]() ,使得
,使得![]()
的某种排列![]() (其中
(其中![]() =
=![]() )依次成等差数列?若存在,求所有的
)依次成等差数列?若存在,求所有的![]()
及相应的![]() ;若不存在,说明理由.
;若不存在,说明理由.
(本题满分14分)已知![]() 是给定的实常数,设函数
是给定的实常数,设函数![]() ,
,![]() ,
,
![]() 是
是![]() 的一个极大值点.
的一个极大值点.
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)设![]() 是
是![]() 的3个极值点,问是否存在实数
的3个极值点,问是否存在实数![]() ,可找到
,可找到![]() ,使得
,使得![]()
的某种排列![]() (其中
(其中![]() =
=![]() )依次成等差数列?若存在,求所有的
)依次成等差数列?若存在,求所有的![]()
及相应的![]() ;若不存在,说明理由.
;若不存在,说明理由.
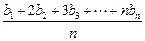 (n∈N*),
(n∈N*), .
. 中,
中, .
. 的值(只写结果)并求出数列
的值(只写结果)并求出数列 ,若对任意的正整数
,若对任意的正整数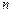 ,当
,当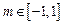 时,不等式
时,不等式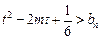 恒成立,求实数
恒成立,求实数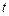 的取值范围。
的取值范围。