摘要:3.. 如图.正三棱柱ABC-A1B1C1的底面边长为2.侧棱长为.A1C1的中点为D. (Ⅰ)求证BC1∥平面AB1D, (Ⅱ)求二面角A1-B1D-A的大小, (Ⅲ)求点B到平面的AB1D的距离. 解:(Ⅰ)连结A1B.设A1B与AB1相交于点O.则O为A1B的中点. 连结DO.因为D为A1C1中点.所以DO为△A1BC1的中位线. 所以DO∥BC1. 又DO平面AB1D.BC1平面AB1D 所以BC1∥平面AB1D. --4分 (Ⅱ)由题意知B1D是正△A1B1C1的中线. 所以A1C1⊥B1D. 在正三棱柱ABC-A1B1C1中.AA1⊥平面A1B1C1 所以AD⊥B1D. 所以∠ADA1是二面角A1-B1D-A的平面角--6分 在Rt△ADA1中. 所以∠ADA1=60°.即二面角A1-B1D-A等于60°. --8分 (Ⅱ)因为O为A1B中点.所以点B到平面AB1D的距离等于点A1到平面AB1D的距 离.由(Ⅱ)可知B1D⊥平面A1ACC1. 所以平面AB1D⊥平面A1ACC1.且平面AB1D∩平面A1ACC1=AD. 过点A1作A1H⊥AD.垂足为H.则A1H⊥平面AB1D. 所以线段A1H的长度就是点A1到平面AB1D的距离. --11分 在Rt△A1AD中. 所以点B到平面AB1D的距离等于 --12分 或设点B到平面AB1D的距离为h.因为 所以 --12分 高考数学中档题精选(6)
网址:http://m.1010jiajiao.com/timu3_id_499076[举报]
(本小题满分12分)
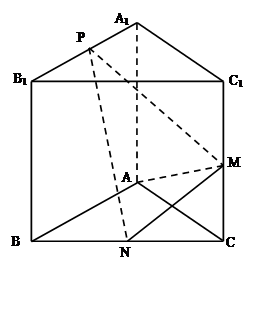
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足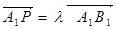
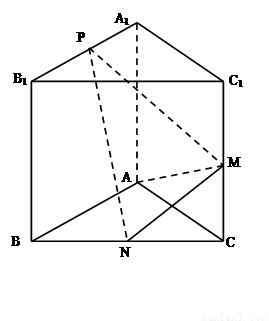
(1)证明:PN⊥AM
(2)若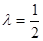 ,求直线AA1与平面PMN所成角的正弦值.
,求直线AA1与平面PMN所成角的正弦值.
查看习题详情和答案>>
( 本小题满分12分)
如图,三棱柱ABC—A1B1C1中,底面为正三角形,侧棱与底面垂直,D是BC的中点,AA1=AB=1。

(1) 求证:A1C∥平面AB1D;
(2) 求点C到平面AB1D的距离。
查看习题详情和答案>>
.(本小题满分12分)
如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点,
(I)求证: AC 1//平面CDB1;
(II)求二面角C1-AB-C的平面角的正切值。

查看习题详情和答案>>

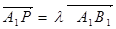
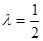 ,求直线AA1与平面PMN所成角的正弦值.
,求直线AA1与平面PMN所成角的正弦值.