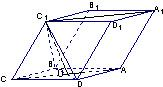
摘要: 如图.已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形.且∠C1CB=∠C1CD=∠BCD=60° ⑴证明:C1C⊥BD, ⑵假定CD=2.CC1=.记面C1BD为α.面CBD为β.求二面角α-BD-β的平面角的余弦值, ⑶当的值为多少时.能使A1C⊥平面C1BD?请给出证明.
网址:http://m.1010jiajiao.com/timu3_id_499058[举报]
如图,已知平行六面体ABCD—A1B1C1D1的底面?ABCD是菱形,且∠C1CB=∠C1CD=∠BCD.
(1)求证: C1C⊥BD![]()
(2)当![]() 的值为多少时,能使A1C⊥平面C1BD?请给出证明.
的值为多少时,能使A1C⊥平面C1BD?请给出证明.
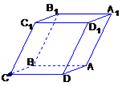
如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且
=
,
=
,
=
,则用
,
,
表示向量
为( )
查看习题详情和答案>>
| OA |
| a |
| OC |
| b |
| OO1 |
| c |
| a |
| b |
| c |
| OG |
A.
| B.
| C.
| D.
|

 如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且
如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且