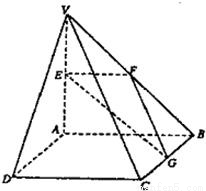
摘要：24． (2005年高考·全国卷Ⅲ·理18文19) 如图.在四棱锥V-ABCD中.底面ABCD是正方形.侧面VAD是正三角形,平面VAD⊥底面ABCD． (Ⅰ)证明AB⊥平面VAD, (Ⅱ)求面VAD与面VDB所成的二面角的大小． 证明:方法一:(Ⅰ)证明: (Ⅱ)解:取VD的中点E.连结AF.BE. ∵△VAD是正三形. ∴AE⊥VD.AE= ∵AB⊥平面VAD. ∴AB⊥AE. 又由三垂线定理知BE⊥VD. 因此.tan∠AEB= 即得所求二面角的大小为 方法二:以D为坐标原点.建立如图所示的坐标图系. (Ⅰ)证明:不防设作A. 则B. . 由得AB⊥VA. 又AB⊥AD.因而AB与平面VAD内两条相交直线VA.AD都垂直. ∴AB⊥平面VAD. (Ⅱ)解:设E为DV中点.则. 由 因此.∠AEB是所求二面角的平面角. 解得所求二面角的大小为
网址：http://m.1010jiajiao.com/timu3_id_498754[举报]
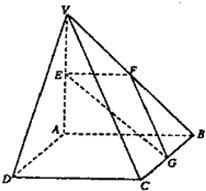如图，在四棱锥V-ABCD中，底面ABCD是矩形，侧棱VA⊥底面ABCD，E、F、G分别为VA、VB、BC的中点．（I）求证：平面EFG∥平面VCD；
（II）当二面角V-BC-A、V-DC-A分别为45°、30°时，求直线VB与平面EFG所成的角． 查看习题详情和答案>>
（本小题满分12分）如图，在四棱锥V—ABCD中，底面ABCD是矩形，侧棱VA⊥底面ABCD，E、F、G分别为VA、VB、BC的中点。（I）求证：平面EFG//平面VCD； （II）当二面角V—BC—A、V—DC—A分别为45°、30°时，求直线VB与平面EFG所成的角。
查看习题详情和答案>>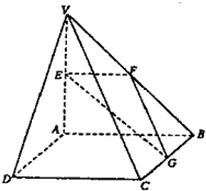
如图，在四棱锥V-ABCD中，底面ABCD是矩形，侧棱VA⊥底面ABCD，E、F、G分别为VA、VB、BC的中点．
