Question

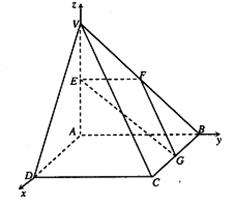
（本小题满分12分）如图，在四棱锥V—ABCD中，底面ABCD是矩形，侧棱VA⊥底面ABCD，E、F、G分别为VA、VB、BC的中点。（I）求证：平面EFG//平面VCD；   （II）当二面角V—BC—A、V—DC—A分别为45°、30°时，求直线VB与平面EFG所成的角。

Answer 1

(Ⅰ)    (Ⅱ)   （Ⅲ）

解析:

（I）∵E、F、G分别为VA、VB、BC的中点，

∴EF//AB，FG//VC，又ABCD是矩形，∴AB//CD，

∴EF//CD，又∵EF平面VCD，FG平面VCD

∴EF//平面VCD，FG//平面VCD，

又EF∩FG=F，∴平面EFG//平面VCD。…4分

 （II）方法一：∵VA⊥平面ABCD，CD⊥AD，∴CD⊥VD。

则∠VDA为二面角V—DC—A的平面角，∠VDA=30°。

同理∠VBA=45°。……7分

作AH⊥VD，垂足为H，由上可知CD⊥平面VAD，则AH⊥平面VCD。

∵AB//平面VCD，∴AH即为B到平面VCD的距离。

由（I）知，平面EFG//平面VCD，则直线VB与平面EFG所成的角等于直线VB与平面VCD所成的角，记这个角为。

………………11分

故直线VB与平面EFG所成的角   ………………12分

方法二：∵VA⊥平面ABCD，CD⊥AD，∴CD⊥VD。

则∠VDA为二面角V—DC—A的平面角，∠VDA=30°。

同理∠VBA=45°。……7分建立如图所示的空间直角坐标系

设平面EFG的法向量为，

则n亦为平面VCD的法向量。

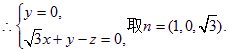
设直线VB与平面EFG所成的角为

则

  11分

故直线VB与平面EFG所成的角  …12分