摘要:20. 已知函数f (x) 是定义在R上的偶函数.当 (Ⅰ)求x<0时.f (x)的解析式, (Ⅱ)试确定函数y= f (x)(x≥0)的单调区间.并证明你的结论, (Ⅲ)(理科学生作.文科学生不作)若 证明:
网址:http://m.1010jiajiao.com/timu3_id_498567[举报]
(本小题满分14分) 已知函数f (x)=ex-k-x,其中x∈R. (1)当k=0时,若g(x)=![]() 定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
(本小题满分14分) 已知函数f (x)=ex-k-x,其中x∈R. (1)当k=0时,若g(x)=![]() 定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
(本小题满分14分) 已知函数f (x)=ex-k-x,其中x∈R. (1)当k=0时,若g(x)= 定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
 定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点. ,(x>0).
,(x>0). 的值 ;
的值 ; 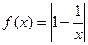 ,(x>0).
,(x>0).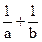 的值 ;
的值 ;  若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [
若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [ ma,mb],(m≠0),求m的取值范围.
ma,mb],(m≠0),求m的取值范围.