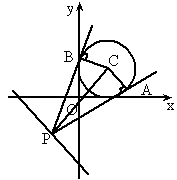
摘要:9.已知P是直线3x+4y+8=0上的动点.PA.PB是圆x2+y2-2x-2y+1=0的两条切线.A.B是切点.C是圆心.那么四边形PACB面积的最小值为 . 解析:设P点坐标为(x.y).则|PC|= .由勾股定理及|AC|=1.得|PA|==. 从而S四边形PACB=2S△PAC=2·|PA|·|AC| =|PA|=. 故欲求S四边形PACB的最小值.只需求|PA|的最小值.即定点C(1,1)与直线上动点P(x.y)的距离的平方的最小值.它也就是点C(1,1)到直线3x+4y+8=0的距离的平方.即这个最小值d2=2=9. ∴S四边形PACB最小值==2. 答案:2
网址:http://m.1010jiajiao.com/timu3_id_497710[举报]
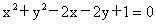 的两条切线,A、B是切点,C是圆心,那么四边
的两条切线,A、B是切点,C是圆心,那么四边