摘要：11．已知椭圆C:+＝1(a>b>0)的离心率为.短轴一个端点到右焦点的距离为. (1)求椭圆C的方程, (2)设直线l与椭圆C交于A.B两点.坐标原点O到直线l的距离为.求△AOB面积的最大值． 解:(1)设椭圆的半焦距为c.依题意 ∴b＝1.∴所求椭圆方程为+y2＝1. (2)设A(x1.y1).B(x2.y2). ①当AB⊥x轴时.|AB|＝. ②当AB与x轴不垂直时.设直线AB的方程为y＝kx+m.由已知＝.得m2＝(k2+1).把y＝kx+m代入椭圆方程.整理得 (3k2+1)x2+6kmx+3m2-3＝0 ∴x1+x2＝.x1x2＝. ∴|AB|2＝(1+k2)(x2-x1)2 ＝(1+k2) ＝＝ ＝3+＝3+(k≠0) ≤3+＝4. 当且仅当9k2＝.即k＝±时等号成立|AB|＝2. 当k＝0时.|AB|＝. 综上所述.|AB|max＝2. ∴当|AB|最大时.△AOB面积取最大值. S＝×|AB|max×＝. 点评:一般地.在涉及直线与曲线交点的问题时.先设出交点的坐标.再由方程组转化的一元二次方程中.利用根与系数的关系转化为待求的系数方程.像这种设交点坐标但不具体求出的方法称为“设而不求 ．
网址：http://m.1010jiajiao.com/timu3_id_497699[举报]
已知椭圆C：
＝1(a＞b＞0)上任一点P到两个焦点的距离的和为2
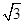，P与椭圆长轴两顶点连线的斜率之积为－
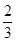.设直线l过椭圆C的右焦点F，交椭圆C于两点A(x1，y1)，B(x2，y2)．
(1)若
＝
(O为坐标原点)，求|y1－y2|的值；
(2)当直线l与两坐标轴都不垂直时，在x轴上是否总存在点Q，使得直线QA，QB的倾斜角互为补角？若存在，求出点Q坐标；若不存在，请说明理由．
已知椭圆C：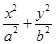
＝1(a＞b＞0)的离心率为
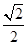，其左、右焦点分别是F1、F2，过点F1的直线l交椭圆C于E、G两点，且△EGF2的周长为4
.
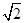(1)求椭圆C的方程；
(2)若过点M(2,0)的直线与椭圆C相交于两点A、B，设P为椭圆上一点，且满足
＋
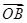＝t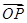
(O为坐标原点)，当|
－
|＜
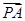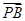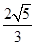时，求实数t的取值范围．
已知椭圆C：
＝1(a＞b＞0)的离心率为
，F为椭圆的右焦点，M、N两点在椭圆C上，且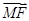
＝λ
(λ＞0)，定点A(－4，0)．
(1)求证：当λ＝1时，
⊥
；
(2)若当λ＝1时，有
·
＝
，求椭圆C的方程．.
＝1(a>b>0)，点A、B分别是椭圆C的左顶点和上顶点，直线AB与圆G：x2＋y2＝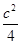
(c是椭圆的半焦距)相离，P是直线AB上一动点，过点P作圆G的两切线，切点分别为M、N.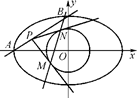
、
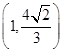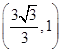，求椭圆C的方程；
·
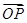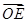的值(O是坐标原点)；
.过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.