若椭圆＝1(m＞n＞0)和双曲线＝1(a＞b＞0)有相同的左、右焦点F₁、F₂，P是两条曲线的一个交点，则|PF₁|·|PF₂|的值是

m－a

(m－a)

m²－a²

设椭圆C₁：的左、右焦点分别是F₁，F₂，下顶点为A，线段OA的中点为B(O为坐标原点)，如图．若抛物线C₂：y＝x²－1与y轴的交点为B，且经过F₁，F₂点．

(1)求椭圆C₁的方程；

(2)设，N为抛物线C₂上的一动点，过点N作抛物线C₂的切线交椭圆C₁于，P，Q两点，求△MPQ面积的最大值．

设椭圆C₁：的左、右焦点分别是F₁，F₂，下顶点为A，线段OA的中点为B(O为坐标原点)，如图．若抛物线C₂：y＝x²－1与y轴的交点为B，且经过F₁，F₂点．

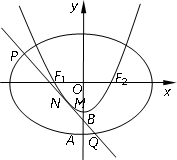
(Ⅰ)求椭圆C₁的方程；

(Ⅱ)设，N为抛物线C₂上的一动点，过点N作抛物线C₂的切线交椭圆C₁于P，Q两点，求△MPQ面积的最大值．

设F₁、F₂分别是椭圆＋y²＝1的左右焦点．

(1)若P是该椭圆上的一个动点，求的最值；

(2)设过定点M(0，2)的直线l与椭圆交于不同的两点A、B，且∠AOB为锐角(O为坐标原点)，求直线l的斜率k的范围．