摘要：1．设斜率为2的直线l过抛物线y2＝ax(a≠0)的焦点F.且和y轴交于点A.若△OAF(O为坐标原点)的面积为4.则抛物线方程为( ) A．y2＝±4 B．y2＝±8x C．y2＝4x D．y2＝8x 解析:y2＝ax的焦点坐标为.过焦点且斜率为2的直线方程为y＝2.令x＝0得:y＝-. ∴×·＝4. ∴a2＝64. ∴a＝±8.故选B. 答案:B
网址：http://m.1010jiajiao.com/timu3_id_497663[举报]
设斜率为2的直线l过抛物线y2＝ax(a≠0)的焦点F，且和y轴交于点A，若△OAF(O为坐标原点)的面积为4，则抛物线的方程为( )
A．y2＝±4x B．y2＝±8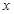
C．y2＝4x D．y2＝8x
查看习题详情和答案>>
设斜率为2的直线l过抛物线y2＝ax(a≠0)的焦点F，且和y轴交于点A，若△OAF(O为坐标原点)的面积为4，则抛物线的方程为( )
A．y2＝±4x
B．y2＝±8
C．y2＝4x D．y2＝8x
查看习题详情和答案>>
设斜率
为2的直线l过抛物线y2＝ax(a≠0)的焦点F，且和y轴交于点A，若△OAF(O为坐标原点)的面积为4，则抛物线方程为( )
(A)y2＝±4x (B)y2＝±8x
(C)y2＝4x (D)y2＝8x
查看习题详情和答案>>设斜率为2的直线l过抛物线y2＝ax(a≠0)的焦点F，且和y轴交于点A，若△OAF(O为坐标原点)的面积为4，则抛物线的方程为( )
| A．y2＝±4x | B．y2＝±8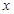 | C．y2＝4x | D．y2＝8x |
设斜率为2的直线l过抛物线y2＝ax(a≠0)的焦点F，且和y轴交于点A，若△OAF(O为坐标原点)的面积为4，则抛物线的方程为( )
| A．y2＝±4x | B．y2＝±8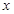 | C．y2＝4x | D．y2＝8x |