摘要：已知三棱柱ABC-A1B1C1的体积为V,E是棱CC1上一点,三棱锥E-ABC的体积是V1,则三棱锥E-A1B1C1的体积是 . 解析:如图,过E作AC､BC的平行线EF､EG,分别与AA1､BB1交于F､G,连接FG. ∵三棱锥E-ABC的体积是V1,∴三棱柱EFG-CAB的体积是3V1, ∴三棱柱EFG-C1A1B1的体积是V-3V1, ∵VE-A1B1C1=VEFG-C1A1B1, ∴VE-A1B1C1= (V-3V1)= -V1. 答案: -V1
网址：http://m.1010jiajiao.com/timu3_id_497657[举报]
已知三棱柱ABC-A1B1C1，侧面AA1C1C⊥侧面ABB1A1，AA1=A1C=CA=2，AB=A1B=| 2 |
（1）求证：AA1⊥BC；
（2）求二面角A-BC-A1的余弦值；
（3）若
| BD |
| DB1 |
面ABC？若存在，求出CE的长；若不存在，请说明理由．
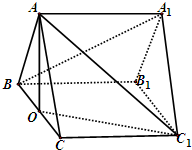（2011•浙江模拟）已知三棱柱ABC-A1B1C1，底面△ABC为正三角形，AA1⊥平面ABC，BC=| 2 |
| 2 |
（Ⅰ）求证：A1B∥平面AOC1；
（Ⅱ）求直线AC与平面AOC1所成角的正弦值．
如图，已知三棱柱ABC-A1B1C1的侧棱与底面所成的角为60°，AB=BC，A1A=A1C=2，AB⊥BC，侧面AA1C1C⊥底面ABC．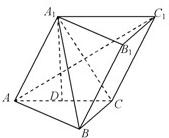
已知三棱柱ABC-A1B1C1，A1在底面ABC上的射影恰为AC的中点D，∠BCA=90°，AC=BC=2，又知BA1⊥AC1