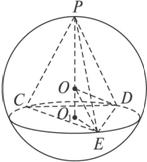
摘要:如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为( ) 解析:由已知条件知,平面图形中AE=EB=BC=CD=DA=DE=EC=1. ∴折叠后得到一个正四面体. 作PF⊥平面DEC,垂足为F,F即为△DEC的中点. 取EC中点G,连接DG、PG, 过球心O作OH⊥平面PEC. 则垂足H为△PEC的中心. ∵PG= ∴OP= ∴外接球体积为π×OP3=×π×π. 答案:C
网址:http://m.1010jiajiao.com/timu3_id_497653[举报]
如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P—DCE的外接球的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P—DCE的外接球的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
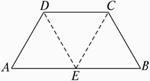
如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点.将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P—DCE的外接球的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
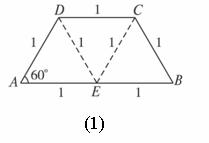
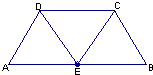 如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为
如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为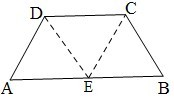 如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则P-DCE三棱锥的外接球的体积为( )
如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则P-DCE三棱锥的外接球的体积为( )