摘要: 已知.如图.在Rt△ABC中.∠C=90º.∠BAC的角平分线AD交BC边于D. (1)以AB边上一点O为圆心.过A.D两点作⊙O(不写作法.保留作图痕迹).再判断直线BC与⊙O的位置关系.并说明理由, 中的⊙O与AB边的另一个交点为E.AB=6.BD=, 求线段BD.BE与劣弧DE所围成的图形面积.(结果保留根号和) [答案](1)如图.作AD的垂直平分线交AB于点O.O为圆心.OA为半径作圆. 判断结果:BC是⊙O的切线.连结OD. ∵AD平分∠BAC ∴∠DAC=∠DAB ∵OA=OD ∴∠ODA=∠DAB ∴∠DAC=∠ODA ∴OD∥AC ∴∠ODB=∠C ∵∠C=90º ∴∠ODB=90º 即:OD⊥BC ∵OD是⊙O的半径 ∴ BC是⊙O的切线. (2) 如图.连结DE. 设⊙O的半径为r.则OB=6-r. 在Rt△ODB中.∠ODB=90º. ∴ 0B2=OD2+BD2 即:(6-r)2= r2+()2 ∴r=2 ∴OB=4 ∴∠OBD=30º.∠DOB=60º ∵△ODB的面积为.扇形ODE的面积为 ∴阴影部分的面积为-.
网址:http://m.1010jiajiao.com/timu3_id_497267[举报]
已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,O是AB的中点,E,F分别在AC,BC上,且ED⊥AC,FD⊥BC.
(1)说出AD=DC=DB的理由;
(2)DE,DF是否相等?请说明理由.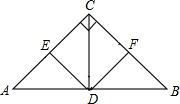
查看习题详情和答案>>
(1)说出AD=DC=DB的理由;
(2)DE,DF是否相等?请说明理由.

已知,如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交BC于点D,过点C作C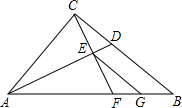 E⊥AD,垂足为E,CE的延长线交AB于点F,过点E作EG∥BC交AB于点G,AE•AD=16,AB=4
E⊥AD,垂足为E,CE的延长线交AB于点F,过点E作EG∥BC交AB于点G,AE•AD=16,AB=4
.
(1)求AC的长;
(2)求EG的长. 查看习题详情和答案>>
 E⊥AD,垂足为E,CE的延长线交AB于点F,过点E作EG∥BC交AB于点G,AE•AD=16,AB=4
E⊥AD,垂足为E,CE的延长线交AB于点F,过点E作EG∥BC交AB于点G,AE•AD=16,AB=4| 5 |
(1)求AC的长;
(2)求EG的长. 查看习题详情和答案>>
 已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.
已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.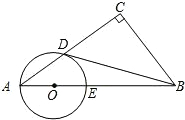 已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.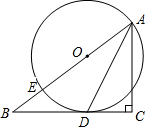 已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,连接AD.
已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,连接AD.