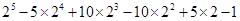摘要: (2011四川凉山州.19.6分)我国古代数学的许多发现都曾位居世界前列.其中“杨辉三角 就是一例.如图.这个三角形的构造法则:两腰上的数都是1.其余每个数均为其上方左右两数之和.它给出了(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如.在三角形中第三行的三个数1.2.1.恰好对应展开式中的系数;第四行的四个数1.3.3.1.恰好对应着展开式中的系数等等. (1)根据上面的规律.写出的展开式. (2)利用上面的规律计算: [答案]解:⑴ ⑵原式= = =1 注:不用以上规律计算不给分.
网址:http://m.1010jiajiao.com/timu3_id_496724[举报]
(2011四川凉山州,19,6分)我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例。如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了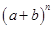 (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应
(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应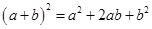 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着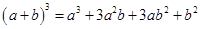 展开式中的系数等等。
展开式中的系数等等。
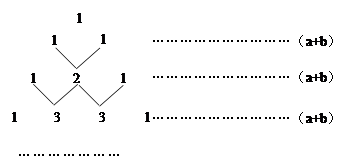

(1)根据上面的规律,写出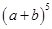 的展开式。
的展开式。
(2)利用上面的规律计算: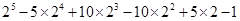 查看习题详情和答案>>
查看习题详情和答案>>
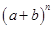 (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应
(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应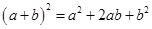 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着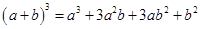 展开式中的系数等等。
展开式中的系数等等。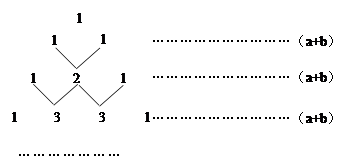

(1)根据上面的规律,写出
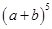 的展开式。
的展开式。(2)利用上面的规律计算:
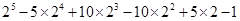 查看习题详情和答案>>
查看习题详情和答案>>
(2011四川凉山州,19,6分)我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例。如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了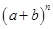 (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应
(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应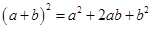 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着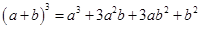 展开式中的系数等等。
展开式中的系数等等。
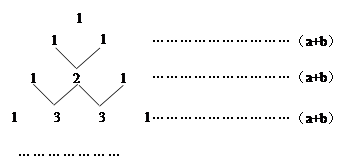

(1)根据上面的规律,写出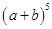 的展开式。
的展开式。
(2)利用上面的规律计算: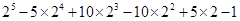 查看习题详情和答案>>
查看习题详情和答案>>
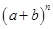 (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应
(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应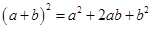 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着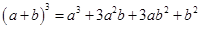 展开式中的系数等等。
展开式中的系数等等。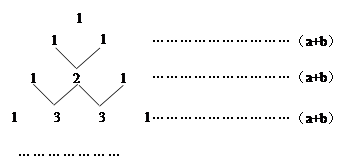

(1)根据上面的规律,写出
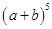 的展开式。
的展开式。(2)利用上面的规律计算:
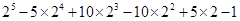 查看习题详情和答案>>
查看习题详情和答案>>
(2011四川凉山州,19,6分)我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例。如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了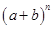 (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应
(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着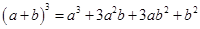 展开式中的系数等等。
展开式中的系数等等。

(1)根据上面的规律,写出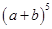 的展开式。
的展开式。
(2)利用上面的规律计算: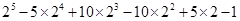
 (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应
(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着 展开式中的系数等等。
展开式中的系数等等。

 的展开式。
的展开式。
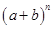 (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应
(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应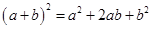 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着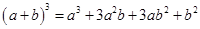 展开式中的系数等等。
展开式中的系数等等。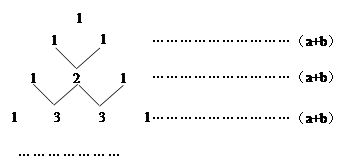

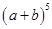 的展开式。
的展开式。