摘要: 如图.已知点D为等腰直角△ABC内一点.∠CAD=∠CBD=15°.E为AD延长线上的一点.且CE=CA. (1)求证:DE平分∠BDC, (2)若点M在DE上.且DC=DM. 求证: ME=BD. [答案](1)在等腰直角△ABC中. ∵∠CAD=∠CBD=15o. ∴∠BAD=∠ABD=45o-15o=30o. ∴BD=AD.∴△BDC≌△ADC. ∴∠DCA=∠DCB=45o. 由∠BDM=∠ABD+∠BAD=30o+30o=60o. ∠EDC=∠DAC+∠DCA=15o+45o=60o. ∴∠BDM=∠EDC. ∴DE平分∠BDC, (2)如图.连接MC. ∵DC=DM.且∠MDC=60°. ∴△MDC是等边三角形.即CM=CD. 又∵∠EMC=180°-∠DMC=180°-60°=120°. ∠ADC=180°-∠MDC=180°-60°=120°. ∴∠EMC=∠ADC. 又∵CE=CA. ∴∠DAC=∠CEM=15°.∴△ADC≌△EMC.∴ME=AD=DB.
网址:http://m.1010jiajiao.com/timu3_id_496619[举报]
 如图,已知点D为等腰直角△ABC内一点,AC=BC,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若DE=acm,BD=bcm(a>b),则CD=
如图,已知点D为等腰直角△ABC内一点,AC=BC,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若DE=acm,BD=bcm(a>b),则CD=a-b
a-b
cm.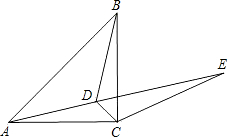 如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°.
如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°.(1)求证:AD=BD;
(2)E为AD延长线上的一点,且CE=CA,求证:AD+CD=DE;
(3)当BD=2时,AC的长为
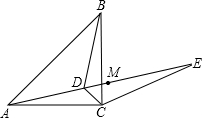 (2012•梁子湖区模拟)如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若点M在DE上,且DC=DM,试探究线段ME与BD的数量关系,并说明理由.
(2012•梁子湖区模拟)如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若点M在DE上,且DC=DM,试探究线段ME与BD的数量关系,并说明理由.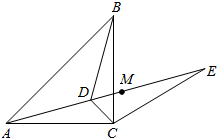 如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.