题目内容
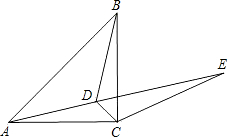 如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°.
如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°.(1)求证:AD=BD;
(2)E为AD延长线上的一点,且CE=CA,求证:AD+CD=DE;
(3)当BD=2时,AC的长为
分析:(1)因为△ABC为等腰直角三角形,∠CAD=∠CBD=15,易证AD=BD;
(2)在DE上截取DM=DC,连接CM,易证△ACD≌△BCD,再根据角与角之间的关系,求得△CMD是等边三角形,则AD+CD=DE可证;
(3)用解直角三角形求得AC的长.
(2)在DE上截取DM=DC,连接CM,易证△ACD≌△BCD,再根据角与角之间的关系,求得△CMD是等边三角形,则AD+CD=DE可证;
(3)用解直角三角形求得AC的长.
解答: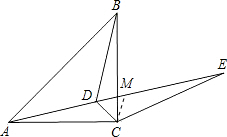 (1)证明:∵AC=BC,∠ACB=90°,
(1)证明:∵AC=BC,∠ACB=90°,
∴∠CAB=∠ABC=45°.
∵∠CAD=∠CBD=15°,
∴∠BAD=∠ABD=30°.
∴AD=BD.
(2)证明:在DE上截取DM=DC,连接CM,
∵AD=BD,AC=BC,DC=DC,
∴△ACD≌△BCD.
∴∠ACD=∠BCD=45°.
∵∠CAD=15°,
∴∠EDC=60°.
∵DM=DC,
∴△CMD是等边三角形.
∴∠CDA=∠CME=120°.
∵CE=CA,
∴∠E=∠CAD.
∴△CAD≌△CEM.
∴ME=AD.
∴DA+DC=ME+MD=DE.
即AD+CD=DE.
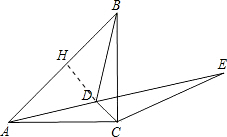
(3)延长CD交AB于点H,则CH⊥AB,
∵∠HBD=30°,BD=2,
∴BH=BD•cos30°=
.
∴AC=BC=BH÷sin45°=
.
 (1)证明:∵AC=BC,∠ACB=90°,
(1)证明:∵AC=BC,∠ACB=90°,∴∠CAB=∠ABC=45°.
∵∠CAD=∠CBD=15°,
∴∠BAD=∠ABD=30°.
∴AD=BD.
(2)证明:在DE上截取DM=DC,连接CM,
∵AD=BD,AC=BC,DC=DC,
∴△ACD≌△BCD.
∴∠ACD=∠BCD=45°.
∵∠CAD=15°,
∴∠EDC=60°.
∵DM=DC,
∴△CMD是等边三角形.
∴∠CDA=∠CME=120°.
∵CE=CA,
∴∠E=∠CAD.
∴△CAD≌△CEM.
∴ME=AD.
∴DA+DC=ME+MD=DE.
即AD+CD=DE.

(3)延长CD交AB于点H,则CH⊥AB,
∵∠HBD=30°,BD=2,
∴BH=BD•cos30°=
| 3 |
∴AC=BC=BH÷sin45°=
| 6 |
点评:本题把全等三角形的判定、等腰三角形的判定和解直角三角形结合求解.综合性强,难度较大,考查学生综合运用数学知识的能力.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
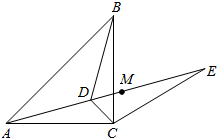 如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.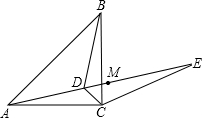 (2012•梁子湖区模拟)如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若点M在DE上,且DC=DM,试探究线段ME与BD的数量关系,并说明理由.
(2012•梁子湖区模拟)如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若点M在DE上,且DC=DM,试探究线段ME与BD的数量关系,并说明理由. 如图,已知点D为等腰直角△ABC内一点,AC=BC,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若DE=acm,BD=bcm(a>b),则CD=
如图,已知点D为等腰直角△ABC内一点,AC=BC,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若DE=acm,BD=bcm(a>b),则CD=