摘要: 如图.△ABC中.AB=AC.AD.CD分别是△ABC两个外角的平分线.在直角梯形ABCD中.AB∥CD.∠ABC=90°.=2CD.对角线AC与BD相交于点O.线段OA.OB的中点分别为点E.F (1)求证:AC=AD, (2)若∠B=60°.求证:四边形ABCD是菱形, [解](1)证明:∵AB=AC. ∴∠B=∠BCA. ∴∠EAC=∠B+∠BCA=2∠B. ∵AD平分∠FAC. ∴∠FAD=∠B. ∴AD∥BC.-------------------------- ∴∠D=∠DCE. ∵CD平分∠ACE. ∴∠ACD=∠DCE. ∴∠D=∠ACD.------------------------ ∴AC=AD,-------------------------- (2)证明:∵∠B=60°. ∴∠ACB=60°.∠FAC=∠ACE=120°. ∴∠DCE=∠B=60°.--------------------- ∴DC∥AB, ∵AD∥BC. ∴四边形ABCD为平行四边形.----------------- 又由(1)知AC=AD. ∴AB=AD. ∴四边形ABCD是菱形.--------------------
网址:http://m.1010jiajiao.com/timu3_id_496559[举报]
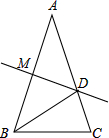 如图,△ABC中,AB=AC,∠A=36°,AB的垂直平分线交AC于D,则下列结论:①∠C=72°;②BD是∠ABC的平分线;③图中共有3个等腰三角形;④AD2=CD•AC,其中正确的有( )
如图,△ABC中,AB=AC,∠A=36°,AB的垂直平分线交AC于D,则下列结论:①∠C=72°;②BD是∠ABC的平分线;③图中共有3个等腰三角形;④AD2=CD•AC,其中正确的有( )
查看习题详情和答案>>
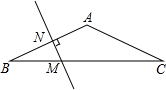 如图,△ABC中,AB=AC,∠C=30゜,AB的垂直平分线MN分别交BC、AB于点M、N,试探究BM与CM之间的数量关系.
如图,△ABC中,AB=AC,∠C=30゜,AB的垂直平分线MN分别交BC、AB于点M、N,试探究BM与CM之间的数量关系.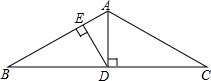 已知,如图,△ABC中,AB=AC,∠BAC=120°,AD⊥BC,DE⊥AB,垂足分别为D,E.求证:BE=3AE.
已知,如图,△ABC中,AB=AC,∠BAC=120°,AD⊥BC,DE⊥AB,垂足分别为D,E.求证:BE=3AE. (2013•铁岭)如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(2013•铁岭)如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE. 如图,△ABC中,AB=BC,∠ABC=90°,△ABC绕B点顺时针旋转至△A1BC1位置,设旋转角为α,0°<α<90°
如图,△ABC中,AB=BC,∠ABC=90°,△ABC绕B点顺时针旋转至△A1BC1位置,设旋转角为α,0°<α<90°