摘要： 在菱形ABCD中.AB=5cm.则此菱形的周长为 A. 5cm B. 15cm C. 20cm D. 25cm [答案]C
网址：http://m.1010jiajiao.com/timu3_id_496498[举报]
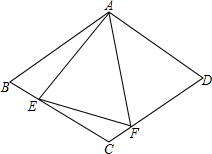如图，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为正三角形，E、F在菱形的边BC，CD上．（1）证明：BE=CF．
（2）当点E，F分别在边BC，CD上移动时（△AEF保持为正三角形），请探究四边形AECF的面积是否发生变化？若不变，求出这个定值；如果变化，求出其最大值．
（3）在（2）的情况下，请探究△CEF的面积是否发生变化？若不变，求出这个定值；如果变化，求出其最大值． 查看习题详情和答案>>
阅读材料：
如图（1），在四边形ABCD中，对角线AC⊥BD，垂足为点O．
求证：S四边形ABCD=
AC•BD；
证明：∵AC⊥BD，
∴S四边形ABCD=S△ACD+S△ACB=
AC•OD+
AC•BO=
AC（OD+OB）=
AC•BD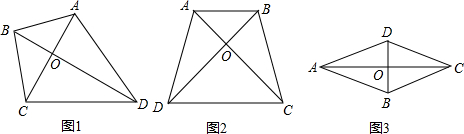
解答下列问题：
（1）上述证明得到的结论可叙述为
（2）如图2，在梯形ABCD中，AB∥CD，AD=BC，AC⊥BD，且AC=8，则S梯形ABCD=
（3）如图3，在菱形ABCD中，AB=5，AC=8，则S菱形ABCD=
查看习题详情和答案>>
如图（1），在四边形ABCD中，对角线AC⊥BD，垂足为点O．
求证：S四边形ABCD=
| 1 |
| 2 |
证明：∵AC⊥BD，
∴S四边形ABCD=S△ACD+S△ACB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答下列问题：
（1）上述证明得到的结论可叙述为
对角线互相垂直的四边形的面积等于对角线乘积的一半
对角线互相垂直的四边形的面积等于对角线乘积的一半
；（2）如图2，在梯形ABCD中，AB∥CD，AD=BC，AC⊥BD，且AC=8，则S梯形ABCD=
32
32
；（3）如图3，在菱形ABCD中，AB=5，AC=8，则S菱形ABCD=
24
24
．
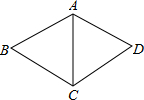（2012•宜昌）如图，在菱形ABCD中，AB=5，∠BCD=120°，则△ABC的周长等于（ ）
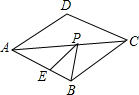如图，在菱形ABCD中，AB=2，∠BAD=60°，E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值为（ ）