摘要： 在△ABC中.∠ACB=90°.∠ABC=30°.将△ABC绕顶点C顺时针旋转.旋转角为(0°＜＜180°).得到△A′B′C． .当AB∥CB′时.设A′B′与CB相交于点D． 证明:△A′CD是等边三角形, .连接A′A.B′B.设△ACA′ 和△BCB′ 的面积分别为S△ACA′ 和S△BCB′． 求证:S△ACA′ :S△BCB′ =1:3, .设AC中点为E.A′B′中点为P.AC=.连接EP.当= °时.EP长度最大.最大值为 ． [答案](1)∵AB∥CB′.∴∠B=∠BC B′=30°.∴∠A′CD=60°. 又∵∠A′=60°.∴∠A′CD=∠A′=∠A′DC=60°.∴△A′CD是等边三角形, (2)∵∠ACA′=∠BCB′.AC=A′C.BC=B′C.∴△ACA′∽△BCB′.相似比为. ∴S△ACA′ :S△BCB′ =1:3, (3)120°.． 当E.C.P三点不共线时.EC+CP>EP, 当E.C.P三点共线时.EC+CP=EP, 综上所述.EP≤EC+CP, 则当旋转120°时.E.C.P三点共线.EP长度最大.此时EP=EC+CP=．
网址：http://m.1010jiajiao.com/timu3_id_496223[举报]
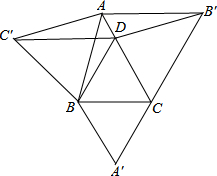如图所示，在△ABC中，∠ACB=60°，AC＞BC，又△ABC′，△BCA′、△CAB′都是△ABC外等边三角形，点D在AC上，且BD=BC．（1）证明：△C′BD≌△B′DC；
（2）证明：△DB′A≌△AC′D；
（3）从△ABC、△A′BC、△AB′C、△ABC′的面积关系上，能得出什么结论？
如图，在△ABC中，∠ACB=90°，CD是斜边AB上的高，ED⊥DF，且DE、DF分别交AC、BC于E、F．
如图，在△ABC中，∠ACB、∠CAB的平分线交于点F，过点F作DE∥AB，分别交BC，BA于D、E．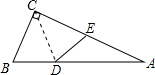
如图，在△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A=28°，则∠ADE=