题目内容

(本小题满分1 0分)

已知：如图，以矩形ABCD的对角线AC的中点O为圆心，OA长为半径作⊙O，⊙O经过B、D两点，过点B作BK⊥ A C，垂足为K。过D作DH∥KB，DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H．

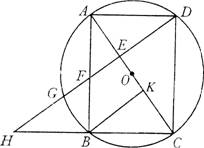
1.(1)求证：AE=CK；

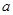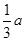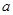    2.(2)如果AB=，AD= (为大于零的常数)，求BK的长：

3.(3)若F是EG的中点，且DE=6，求⊙O的半径和GH的长．

 

【答案】

 

1.（1）证明△AED≌△CKB

2.（2）BK=

3.（3）设GF=x，则EF=x,ED=BK=6,

由射影定理得AE=KC=

由相交弦定理得，

∴

∴

∴

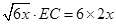
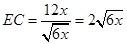
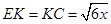
∴K为EC的中点

∴,∴

∴

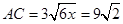
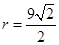
显然，HE=2BK=12

∴HG=6

 

【解析】略

 

练习册系列答案
相关题目
（本小题满分6分，请在下列两个小题中，任选其一完成即可）
（1）解方程：x2+3x-2=0；
（2）如图，在边长为1个单位长度的正方形方格纸中建立直角坐标系，△ABC各顶点的坐标为：A（-5，4）、B（-1，1）、C（-5，1）．
①将△ABC绕着原点O顺时针旋转90°得到△A′B′C′，请在图中画出△A′B′C′；
②写出A′点的坐标．
加试题（本小题满分20分，其中（1）、（2）、（3）题各3分，（4）题11分）
（1）一个正数的平方根为3-a和2a+3，则这个正数是
81
81

（2）若x2+2x+y2-6y+10=0，则xy=
-1
-1

（3）已知a，b分别是6-
13
的整数部分和小数部分，则2a-b=
13
13

（4）阅读下面的问题，并解答问题：
1）如图1，等边△ABC内有一点P，若点P到顶点A，B，C的距离分别为3，4，5，求∠APB的度数是多少？（请在下列横线上填上合适的答案）
分析：由于PA，PB，PC不在同一个三角形中，为了解决本题我们可以将△ABP绕顶点A逆时针旋转到△ACP′处，此时可以利用旋转的特征等知识得到：
  ①∠APB=∠AP′C=∠AP′P+∠PP′C；
  ②AP=AP′，且∠PAP′=
60
60
度，所以△APP′为
等边
等边
三角形，则∠AP′P=
60
60
度；
  ③P′C=BP=4，P′P=AP=3，PC=5，所以△PP′C为
直角
直角
三角形，则∠PP′C=
90
90
度，从而得到∠APB=
150
150
度．
 2）请你利用第1）题的解答方法，完成下面问题：
如图2，在△ABC中，∠CAB=90°，AB=AC，E、F为边BC上的点，且∠EAF=45°，试说明：EF2=BE2+FC2．

（本小题满分5分）
先化简，再选择一个你喜欢又使原式有意义的数代入求值.

（2011广西崇左，19，7分）（本小题满分7分）解不等式组，并
把它的解集在数轴上表示出来.

（本小题满分8分）
据2010年5月8日《杭州日报》报道：今年“五一”黄金周期间，我市实现旅游收入再创历史新高，旅游消费呈现多样化，各项消费所占的比例如图秘所示，其中住宿消费为3438．24万元．
（1）求我市今年“五一”黄金周期间旅游消费共多少亿元？旅游消费中各项消费的中位数是多少万元？
（2）对于“五一”黄金周期间的旅游消费，如果我市2012年要达到3．42亿元的目标，那么，2010年到2012年的平均增长率是多少？
2010年杭州市“五一”黄金周旅游各项消费分布统计图

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网