摘要： 在△ABC中.∠C＝90°.AC＝3cm.BC＝4cm.若⊙A.⊙B的半径分别为1cm.4cm.则⊙A.⊙B的位置关系是 A.外切 B.内切 C.相交 D.外离 [答案]A
网址：http://m.1010jiajiao.com/timu3_id_496003[举报]
如图，在△ABC中，AB＝AC，AE是角平分线，BM平分∠ABC交AE于点M，经过B、M两点的⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径．
【小题1】判断AE与⊙O的位置关系，并说明理由；
【小题2】当BC＝4，AC＝3CE时，求⊙O的半径．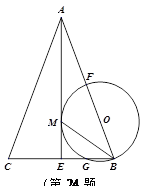
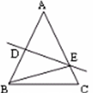
(1)如图1，在△ABC中，BA＝BC，D，E是AC边上的两点，且满足∠DBE＝
∠ABC(0°＜∠CBE＜∠ABC)，以点B为旋转中心，将△BEC按逆时针旋转，得到△BE′A(点C与点A重合，点E到点E′处)连接DE′.
求证：DE′＝DE.
(2)如图2，在△ABC中，BA＝BC，∠ABC＝90°，D，E是AC边上的两点，且满足∠DBE＝∠ABC(0°＜∠CBE＜∠45°)．
求证：DE2＝AD2＋EC2.
∠ABC(0°＜∠CBE＜∠ABC)，以点B为旋转中心，将△BEC按逆时针旋转，得到△BE′A(点C与点A重合，点E到点E′处)连接DE′.求证：DE′＝DE.
(2)如图2，在△ABC中，BA＝BC，∠ABC＝90°，D，E是AC边上的两点，且满足∠DBE＝
∠ABC(0°＜∠CBE＜∠45°)．求证：DE2＝AD2＋EC2.
