摘要: 如图.已知反比例函数的图象经过点(.8).直线经过该反比例函数图象上的点Q(4.). (1)求上述反比例函数和直线的函数表达式, (2)设该直线与轴.轴分别相交于A .B两点.与反比例函数图象的另一个交点为P.连结0P.OQ.求△OPQ的面积. [答案]解:(1)由反比例函数的图象经过点(.8).可知.所以反比例函数解析式为.∵点Q是反比例函数和直线的交点.∴.∴点Q的坐标是(4.1).∴.∴直线的解析式为. (2)如图所示:由直线的解析式可知与轴和轴交点坐标点A与点B的坐标分别为.由反比例函数与直线的解析式可知两图像的交点坐标分别点P(1.4)和点Q(4.1).过点P作PC⊥轴.垂足为C.过点Q作QD⊥轴.垂足为D. ∴S△OPQ=S△AOB-S△OAQ-S△OBP =×OA×OB-×OA×QD-×OB×PC =×25-×5×1-×5×1=.
网址:http://m.1010jiajiao.com/timu3_id_495476[举报]
如图,已知反比例函数y1=
和一次函数y2=ax+b的图象相交于第一象限内的点A,且点A的横坐标为1.过点A作AB⊥x轴于点B,△AOB的面积为2.一次函数y2=ax+b的图象与x轴相交于点C,且三角形ABC是等腰直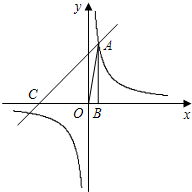 角三角形.
角三角形.
(1)求反比例函数和一次函数的解析式;
(2)结合图象直接写出:当y1>y2时,x的取值范围. 查看习题详情和答案>>
| k | x |
 角三角形.
角三角形.(1)求反比例函数和一次函数的解析式;
(2)结合图象直接写出:当y1>y2时,x的取值范围. 查看习题详情和答案>>
 (2012•门头沟区二模)如图,已知反比例函数y=
(2012•门头沟区二模)如图,已知反比例函数y=| 6 | x |
(1)求一次函数的解析式;
(2)结合图象回答:反比例函数的值大于一次函数的值时x的取值范围.
 如图,已知反比例函数y=
如图,已知反比例函数y=| k | 2x |
(1)求A点坐标及反比例函数的解析式;
(2)请问:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.
 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,已知反比例函数y=
如图,已知反比例函数y=