题目内容
(2013•湖州一模)如图①是矩形包书纸的示意图,虚线是折痕,四个角均为大小相同的正方形,正方形的边长为折叠进去的宽度.
(1)现有一本书长为25cm,宽为20cm,厚度是2cm,如果按照如图①的包书方式,并且折叠进去的宽度是3cm,则需要包书纸的长和宽分别为多少?(请直接写出答案).
(2)已知数学课本长为26cm,宽为18.5cm,厚为1cm,小明用一张面积为1260cm2 的矩形包书纸按如图①包好了这本书,求折进去的宽度.
(3)如图②,矩形ABCD是一张一个角(△AEF)被污损的包书纸,已知AB=30,BC=50,AE=12,AF=16,要使用没有污损的部分包一本长为19,宽为16,厚为6的字典,小红认为只要按如图②的剪裁方式剪出一张面积最大的矩形PGCH就能包好这本字典.设PM=x,矩形PGCH的面积为y,当x取何值时y最大?并由此判断小红的想法是否可行.

(1)现有一本书长为25cm,宽为20cm,厚度是2cm,如果按照如图①的包书方式,并且折叠进去的宽度是3cm,则需要包书纸的长和宽分别为多少?(请直接写出答案).
(2)已知数学课本长为26cm,宽为18.5cm,厚为1cm,小明用一张面积为1260cm2 的矩形包书纸按如图①包好了这本书,求折进去的宽度.
(3)如图②,矩形ABCD是一张一个角(△AEF)被污损的包书纸,已知AB=30,BC=50,AE=12,AF=16,要使用没有污损的部分包一本长为19,宽为16,厚为6的字典,小红认为只要按如图②的剪裁方式剪出一张面积最大的矩形PGCH就能包好这本字典.设PM=x,矩形PGCH的面积为y,当x取何值时y最大?并由此判断小红的想法是否可行.

分析:(1)仔细分析题意及图形的特征即可得到结果;
(2)设折进去的宽度为xcm,根据“长为26 cm,宽为18.5cm,厚为1cm,矩形的面积为1260cm2”及可列方程求解,要注意解的取舍;
(3)先由题意表示出EM,再根据矩形的面积公式得到y与x的函数关系式,最后根据二次函数的性质求解即可.
(2)设折进去的宽度为xcm,根据“长为26 cm,宽为18.5cm,厚为1cm,矩形的面积为1260cm2”及可列方程求解,要注意解的取舍;
(3)先由题意表示出EM,再根据矩形的面积公式得到y与x的函数关系式,最后根据二次函数的性质求解即可.
解答:解:(1)20×2+2+3×2=48cm
25+3×2=31cm
答:包书纸的长和宽分别为48cm、31cm;
(2)设折进去的宽度为xcm,由题意得
(18.5×2+1+2x)(26+2x)=1260
化简得x2+32x-68=0
解得x1=2,x2=-34(不合题意,舍去)
答:折进去的宽度为2cm;
(3)由题意得EM=
x,
所以y=(50-x)(30-12+
x)
整理得y=-
x2+
x+900=-
(x-13)2+
当x=13时,y最大
因为50-13=37<16×2+6=38
所以小红的想法不可行.
25+3×2=31cm
答:包书纸的长和宽分别为48cm、31cm;
(2)设折进去的宽度为xcm,由题意得
(18.5×2+1+2x)(26+2x)=1260
化简得x2+32x-68=0
解得x1=2,x2=-34(不合题意,舍去)
答:折进去的宽度为2cm;
(3)由题意得EM=
| 3 |
| 4 |
所以y=(50-x)(30-12+
| 3 |
| 4 |
整理得y=-
| 3 |
| 4 |
| 39 |
| 2 |
| 3 |
| 4 |
| 3093 |
| 4 |
当x=13时,y最大
因为50-13=37<16×2+6=38
所以小红的想法不可行.
点评:考查了二次函数的应用,二次函数的应用是初中数学的重点和难点,是中考常见题,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
 (2013•湖州一模)如图,一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,它的母线长是5米,底面半径为3米,则做这把遮阳伞需用布料的面积是( )平方米(接缝不计)
(2013•湖州一模)如图,一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,它的母线长是5米,底面半径为3米,则做这把遮阳伞需用布料的面积是( )平方米(接缝不计)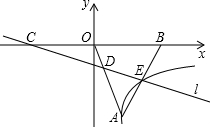 (2013•湖州一模)如图,△AOB为等边三角形,点A在第四象限,点B的坐标为(4,0),过点C(-4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数x图象上,当△ADE和△DCO的面积相等时,k的值为( )
(2013•湖州一模)如图,△AOB为等边三角形,点A在第四象限,点B的坐标为(4,0),过点C(-4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数x图象上,当△ADE和△DCO的面积相等时,k的值为( )