题目内容
 如图,直线y=2x-4与x轴交于点A,与y轴交于点B,以x轴上点M为圆心,过A、B两点作⊙M与x轴交于另一点C.
如图,直线y=2x-4与x轴交于点A,与y轴交于点B,以x轴上点M为圆心,过A、B两点作⊙M与x轴交于另一点C.(1)求⊙M的半径及圆心M的坐标;
(2)①求经过A、B、C三点的抛物线的顶点D的坐标;
②求证:DB是⊙M的切线;
(3)若半径为1的⊙P与x轴和直线BD都相切,请直接写出点P的坐标.
分析:(1)根据题意,连接BC可得AC是⊙O直径,进而可得OB2=OA•OC,进而可得圆心的坐标与半径的大小;
(2)设出其解析式,并用三点式求抛物线解析可得答案;
(3)根据题意,半径为1的⊙P与x轴相切,故P的纵坐标的绝对值为1,即为±1,将其值代入抛物线解析式,即可得到其横坐标,综合可以写出P的坐标.
(2)设出其解析式,并用三点式求抛物线解析可得答案;
(3)根据题意,半径为1的⊙P与x轴相切,故P的纵坐标的绝对值为1,即为±1,将其值代入抛物线解析式,即可得到其横坐标,综合可以写出P的坐标.
解答:解:(1)y=2x-4与x轴交于点A(2,0),与y轴交于点B(0,-4).(1分)
解法(一):连接BC,
∵AC是⊙O直径,
∴∠ABC=90°OB⊥AC.
∴OB2=OA•OC.
即42=2OC.
∴OC=8.
∴直径AC=8+2=10.
∴半径R=5,圆心M坐标(-3,0).(3分)
解法(二):连接MB,易知MB2=MO2+BO2
即R2=(R-2)2+42,
∴R=5.
∴圆心M坐标为(-5,0).
解法(三):M点是AB的中垂线与x轴的交点,
AB:y=2x-4故可设中垂线y=-
x+b过AB中点(1,-2),
故y=-
x-
.
∴圆心M坐标为(-5,0)
∴半径R=3+2=5.
(解法(二)、(三)参考给分)
(2)①设过A(2,0),B(0,-4),C(-8,0)的解析式为y=a(x-2)(x+8),
∴-4=a(0-2)(0+8).
∴a=
.
∴y=
(x-2)(x+8)=
x2+
x-4(5分)
=
(x+3)2-
.(6分)
∴顶点D的坐标为(-3,-
).(7分)
(用三点式求抛物线解析式参考给分)
②解法(一):
连MD、MBl则MD2=(
)2=
&MB2+BD2=52+(
-4)2+32=
,
∴MD2=MB2+BD2
∴∠MBD=90°.
∴BD是⊙M的切线.(8分)
解法(二):直线MB过点M(-3,0)、B(0,-4),
∴y=-
x-4.
直线BD过点D(-3,-
)、B(0,-4)
∴y=
x-4.
∵k1k2=-
×
=-1,
∴直线MB与DB垂直.
∴BD是⊙M的切线.
(其它解法参考给分)
(3)P1(
,1)、P2(
,-1)、P3(
,-1)、P4(5,1)(12分)
(写一个点坐标给1分).
解法(一):连接BC,
∵AC是⊙O直径,
∴∠ABC=90°OB⊥AC.
∴OB2=OA•OC.
即42=2OC.
∴OC=8.
∴直径AC=8+2=10.
∴半径R=5,圆心M坐标(-3,0).(3分)
解法(二):连接MB,易知MB2=MO2+BO2
即R2=(R-2)2+42,
∴R=5.
∴圆心M坐标为(-5,0).
解法(三):M点是AB的中垂线与x轴的交点,
AB:y=2x-4故可设中垂线y=-
| 1 |
| 2 |
故y=-
| 1 |
| 2 |
| 3 |
| 2 |
∴圆心M坐标为(-5,0)
∴半径R=3+2=5.
(解法(二)、(三)参考给分)
(2)①设过A(2,0),B(0,-4),C(-8,0)的解析式为y=a(x-2)(x+8),
∴-4=a(0-2)(0+8).
∴a=
| 1 |
| 4 |
∴y=
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
=
| 1 |
| 4 |
| 25 |
| 4 |
∴顶点D的坐标为(-3,-
| 25 |
| 4 |
(用三点式求抛物线解析式参考给分)
②解法(一):
连MD、MBl则MD2=(
| 25 |
| 4 |
| 625 |
| 16 |
| 25 |
| 4 |
| 625 |
| 16 |
∴MD2=MB2+BD2
∴∠MBD=90°.
∴BD是⊙M的切线.(8分)
解法(二):直线MB过点M(-3,0)、B(0,-4),
∴y=-
| 4 |
| 3 |
直线BD过点D(-3,-
| 25 |
| 4 |
∴y=
| 3 |
| 4 |
∵k1k2=-
| 4 |
| 3 |
| 3 |
| 4 |
∴直线MB与DB垂直.
∴BD是⊙M的切线.
(其它解法参考给分)
(3)P1(
| 25 |
| 3 |
| 17 |
| 3 |
| 7 |
| 3 |
(写一个点坐标给1分).
点评:本题考查学生将二次函数的图象与解析式相结合处理问题、解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
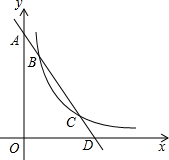 如图,直线y=-2x+b与y轴交于点A,与x轴交于点D,与双曲线
如图,直线y=-2x+b与y轴交于点A,与x轴交于点D,与双曲线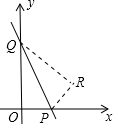 如图,直线y=-2x+6与x轴、y轴分别交于P、Q两点,把△POQ沿PQ翻折,点O落在R处,则点R的坐标是
如图,直线y=-2x+6与x轴、y轴分别交于P、Q两点,把△POQ沿PQ翻折,点O落在R处,则点R的坐标是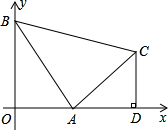 腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D.
腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D. 轴分别交于点C、D.直线EB交x轴于点F.
轴分别交于点C、D.直线EB交x轴于点F. 如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.
如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.