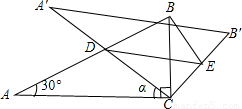
题目内容
如图,将含30°角的直角三角板ABC(∠B=30°)绕其直角顶点A逆时针旋转α解(0°<α<90°),得到Rt△ADE,AD与BC相交于点M,过点M作MN∥DE交AE于点N,连接NC.设BC=4,BM=x,△MNC的面积为S△MNC,△ABC的面积为S△ABC.(1)求证:△MNC是直角三角形;
(2)试求用x表示S△MNC的函数关系式,并写出x的取值范围;
(3)以点N为圆心,NC为半径作⊙N,
①当直线AD与⊙N相切时,试探求S△MNC与S△ABC之间的关系;
②当S△MNC=
 S△ABC时,试判断直线AD与⊙N的位置关系,并说明理由.
S△ABC时,试判断直线AD与⊙N的位置关系,并说明理由.
【答案】分析:(1)利用平行线的性质和等量代换,易得△ABM∽△ACN,再由等量代换得到∠MCN=90°即可;
(2)由于△MNC是直角三角形,则有S△MNC= MN•CN,而MC=4-x,故利用相似三角形的对应边成比例用含x的代数式表示出CN,就可求得S△MNC的函数关系式.
MN•CN,而MC=4-x,故利用相似三角形的对应边成比例用含x的代数式表示出CN,就可求得S△MNC的函数关系式.
(3)①当直线AD与⊙N相切时,利用AN=NC,确定出CN的值后,用2中的S△MNC的函数关系式,确定S△MNC与S△ABC之间的关系;②当S△MNC= S△ABC时,求得x的值,讨论x取不同值时直线AD与⊙N的位置关系.
S△ABC时,求得x的值,讨论x取不同值时直线AD与⊙N的位置关系.
解答:解:(1)MN∥DE,∴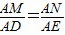 ,
,
又∵AD=AB,AE=AC,∴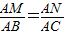 ,
,
又∵∠BAM=∠CAN,∴△ABM∽△ACN,
∴∠B=∠NCA,∴∠NCA+∠ACB=∠B+∠ACB=90°,
∴∠MCN=90°.即△MNC是直角三角形.
(2)在Rt△ABC中,∠A=90°,∠B=30°,BC=4,
∴AC=2,AB=2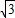 ,
,
∴△ABM∽△ACN,∴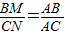 ,
,
∴ ,
,
∴S△MNC= CM•CN=
CM•CN= (4-x)•
(4-x)•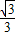 x=
x=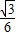 (4x-x2)(0<x<4).
(4x-x2)(0<x<4).
(3)①直线AD与⊙N相切时,则AN=NC,
∵△ABM∽△ACN,
∴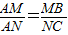 ,∴AM=MB.
,∴AM=MB.
∵∠B=30°∴∠α=30°,∠AMC=60°.
又∵∠ACB=90°-30°=60°
∴△AMC是等边三角形,有AM=MC=BM= BC=2,即x=2.
BC=2,即x=2.
S△MNC=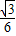 (4x-x2)=
(4x-x2)=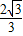 ,∵S△ABC=
,∵S△ABC= AB•AC=2
AB•AC=2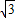 ,
,
∴S△MNC= S△ABC.
S△ABC.
②当S△MNC= S△ABC时
S△ABC时
∴S△MNC=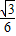 (4x-x2)=
(4x-x2)=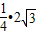 解得x=1或x=3.
解得x=1或x=3.
(i)当x=1时,
在Rt△MNC中,MC=4-x=3,∴MN=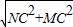 =
=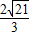
∵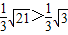 ,即AN>NC,
,即AN>NC,
∴直线AD与⊙相离.
(ii)当x=3时,
同理可求出,NC=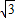 ,MC=1,MN=2,AN=1
,MC=1,MN=2,AN=1
∴NC>AN
∴直线AD与⊙相交.
点评:本题利用了平行线的性质,相似三角形的判定和性质,三角形的面积公式,直角三角形的性质求解,运用了分类讨论的思想.
(2)由于△MNC是直角三角形,则有S△MNC=
 MN•CN,而MC=4-x,故利用相似三角形的对应边成比例用含x的代数式表示出CN,就可求得S△MNC的函数关系式.
MN•CN,而MC=4-x,故利用相似三角形的对应边成比例用含x的代数式表示出CN,就可求得S△MNC的函数关系式.(3)①当直线AD与⊙N相切时,利用AN=NC,确定出CN的值后,用2中的S△MNC的函数关系式,确定S△MNC与S△ABC之间的关系;②当S△MNC=
 S△ABC时,求得x的值,讨论x取不同值时直线AD与⊙N的位置关系.
S△ABC时,求得x的值,讨论x取不同值时直线AD与⊙N的位置关系.解答:解:(1)MN∥DE,∴
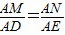 ,
,又∵AD=AB,AE=AC,∴
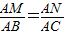 ,
,又∵∠BAM=∠CAN,∴△ABM∽△ACN,
∴∠B=∠NCA,∴∠NCA+∠ACB=∠B+∠ACB=90°,
∴∠MCN=90°.即△MNC是直角三角形.
(2)在Rt△ABC中,∠A=90°,∠B=30°,BC=4,
∴AC=2,AB=2
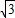 ,
,∴△ABM∽△ACN,∴
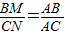 ,
,∴
 ,
,∴S△MNC=
 CM•CN=
CM•CN= (4-x)•
(4-x)•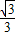 x=
x=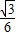 (4x-x2)(0<x<4).
(4x-x2)(0<x<4).(3)①直线AD与⊙N相切时,则AN=NC,
∵△ABM∽△ACN,
∴
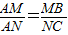 ,∴AM=MB.
,∴AM=MB.∵∠B=30°∴∠α=30°,∠AMC=60°.
又∵∠ACB=90°-30°=60°
∴△AMC是等边三角形,有AM=MC=BM=
 BC=2,即x=2.
BC=2,即x=2.S△MNC=
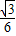 (4x-x2)=
(4x-x2)=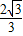 ,∵S△ABC=
,∵S△ABC= AB•AC=2
AB•AC=2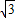 ,
,∴S△MNC=
 S△ABC.
S△ABC.②当S△MNC=
 S△ABC时
S△ABC时∴S△MNC=
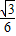 (4x-x2)=
(4x-x2)=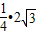 解得x=1或x=3.
解得x=1或x=3.(i)当x=1时,
在Rt△MNC中,MC=4-x=3,∴MN=
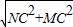 =
=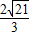
∵
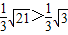 ,即AN>NC,
,即AN>NC,∴直线AD与⊙相离.
(ii)当x=3时,
同理可求出,NC=
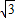 ,MC=1,MN=2,AN=1
,MC=1,MN=2,AN=1∴NC>AN
∴直线AD与⊙相交.
点评:本题利用了平行线的性质,相似三角形的判定和性质,三角形的面积公式,直角三角形的性质求解,运用了分类讨论的思想.

练习册系列答案
相关题目
 C,△ABC的面积为S△ABC.
C,△ABC的面积为S△ABC. 交CB′于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.
交CB′于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.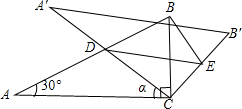 交CB′于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.
交CB′于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.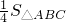 时,判断⊙E与A′C的位置关系,并求相应的tanα值.
时,判断⊙E与A′C的位置关系,并求相应的tanα值.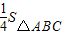 时,判断⊙E与A′C的位置关系,并求相应的tanα值.
时,判断⊙E与A′C的位置关系,并求相应的tanα值.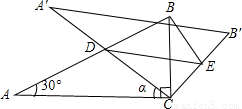
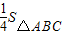 时,判断⊙E与A′C的位置关系,并求相应的tanα值.
时,判断⊙E与A′C的位置关系,并求相应的tanα值.