摘要: 在复习一课时.同桌的小明和小芳有一个问题观点不一致.小明认为如果两次分别从1-6六个整数中任取一个数.第一个数作为点的横坐标.第二个数作为点的纵坐标.则点在反比例函数的图象上的概率一定大于在反比例函数的图象上的概率.而小芳却认为两者的概率相同.你赞成谁的观点? (1)试用列表或画树状图的方法列举出所有点的情形, (2)分别求出点在两个反比例函数的图象上的概率.并说明谁的观点正确. [答案]解: (1)列表如下: ------------------------6分 第二个数 第一个数 1 2 3 4 5 6 1 (1.6) 2 (2.6) 3 (3.6) 4 (4.6) 5 (5.1) (5.2) (5.6) 6 (6.2) (6.6) 画树状图如下: ------------------------6分 (2)由树状图或表格可知.点共有36种可能的结果.且每种结果出现的可能性相同.点.(6,2)在反比例函数的图象上.-----7分 点 .(6,1)在反比例函数的图象上, -------8分 故点在反比例函数和的图象上的概率相同,都是---9分 所以小芳的观点正确. ------------------------10分
网址:http://m.1010jiajiao.com/timu3_id_495233[举报]
在复习《反比例函数》一课时,同桌的小明和小芳有一个问题观点不一致.小明认为如果两次分别从1~6六个整数中任取一个数,第一个数作为点P(m,n)的横坐标,第二个数作为点P(m,n)的纵坐标,则点P(m,n)在反比例函数y=
的图象上的概率一定大于在反比例函数y=
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
(1)试用列表或画树状图的方法列举出所有点P(m,n)的情形;
(2)分别求出点P(m,n)在两个反比例函数的图象上的概率,并说明谁的观点正确. 查看习题详情和答案>>
| 12 |
| x |
| 6 |
| x |
(1)试用列表或画树状图的方法列举出所有点P(m,n)的情形;
(2)分别求出点P(m,n)在两个反比例函数的图象上的概率,并说明谁的观点正确. 查看习题详情和答案>>
(2013•黄冈模拟)在复习《反比例函数》一课时,同桌的小峰和小轩有一个问题观点不一致:
情境:随机同时掷两枚质地均匀的骰子(骰子六个面上的点数分别代表1,2,3,4,5,6).第一枚骰子上的点数作为点P(m,n)的横坐标,第二枚骰子上的点数作为P(m,n)的纵坐标.
小峰认为:点P(m,n)在反比例函数y=
图象上的概率一定大于在反比例函数y=
图象上的概率;
小轩认为:P(m,n)在反比例函数y=
和y=
图象上的概率相同.
问题:(1)试用列表或画树状图的方法,列举出所有点P(m,n)的情形;
(2)分别求出点P(m,n)在两个反比例函数的图象上的概率,并说明谁的观点正确.
查看习题详情和答案>>
情境:随机同时掷两枚质地均匀的骰子(骰子六个面上的点数分别代表1,2,3,4,5,6).第一枚骰子上的点数作为点P(m,n)的横坐标,第二枚骰子上的点数作为P(m,n)的纵坐标.
小峰认为:点P(m,n)在反比例函数y=
| 8 |
| x |
| 6 |
| x |
小轩认为:P(m,n)在反比例函数y=
| 8 |
| x |
| 6 |
| x |
问题:(1)试用列表或画树状图的方法,列举出所有点P(m,n)的情形;
(2)分别求出点P(m,n)在两个反比例函数的图象上的概率,并说明谁的观点正确.
(本小题满分10分)
在复习《反比例函数》一课时,同桌的小明和小芳有一个间题观点不一致,小明认为如果两次分别从l到6六个整数中任取一个数,第一个数作为点 的横坐标,第二个数作为点
的横坐标,第二个数作为点 的纵坐标,则点
的纵坐标,则点 在反比例函数
在反比例函数 的的图象上的概率一定大于在反比例函数
的的图象上的概率一定大于在反比例函数 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
(1)试用列表或画树状图的方法列举出所有点 的情形;
的情形;
(2)分别求出点 在两个反比例函数的图象上的概率,并说明谁的观点正确。
在两个反比例函数的图象上的概率,并说明谁的观点正确。
 的横坐标,第二个数作为点
的横坐标,第二个数作为点 的图象上的概率一定大于在反比例函数
的图象上的概率一定大于在反比例函数 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点? 的横坐标,第二个数作为点
的横坐标,第二个数作为点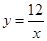 的图象上的概率一定大于在反比例函数
的图象上的概率一定大于在反比例函数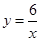 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?