摘要:27.如图.已知O.动点P从O点出发.以每秒3个单位的速度.沿△OAB的边0A.AB.B0作匀速运动,动直线l从AB位置出发.以每秒1个单位的速度向x轴负方向作匀速平移运动.若它们同时出发.运动的时间为t秒.当点P运动到O时.它们都停止运动. (1)当P在线段OA上运动时.求直线l与以P为圆心.1为半径的圆相交时t的取值范围, (2)当P在线段AB上运动时.设直线l分到与OA.OB交于C.D.试问:四边形CPBD是否可能为菱形?若能.求出此时t的值,若不能.请说明理由.并说明如何改变直线l的出发时间.使得四边形CPBD会是菱形. [答案]解: (1)设经过t秒,P点坐标为, 直线l从AB位置向x轴负方向作匀速平移运动时与x轴交点为F,则∵圆的半径为1,∴要直线l与圆相交即要 ∴当F在P左侧,PF的距离为 当F在P左侧,PF的距离为 ∴当P在线段OA上运动时.直线l与以P为圆心.1为半径的圆相交时t的取值范围为. (2) 当P在线段AB上运动时.设直线l分别与OA.OB交于C.D.不可能为菱形.理由是:易知CA=t,PA=3t-4,OB=5 从上可知,PB:CB:PC=3:4:5, 故设PB=3m, CB=4m,PC=5m, 则AP=3-3m 由 令 即将直线l的出发时间推迟秒,四边形CPBD会是菱形. [考点]圆与直线的位置关系, 相似, 菱形的判定, 待定系数法. [分析](1) 利用直线l与圆相交的条件可以得知结果. (2)①利用邻边相等的平行四边形是菱形的思路, 首先找出,四边形CPBD是平行四边形的条件, 再分别求出一组邻边的长来判定能不能构成菱形. ②利用待定系数法来寻求,
网址:http://m.1010jiajiao.com/timu3_id_495167[举报]
(本题满分10分)如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE、CD相交于点B.

(1)求证:直线AB是⊙O的切线.
(2)当AC=1,BE=2时,求tan∠OAC的值.
查看习题详情和答案>>
(本题满分10分)
如图,已知正比例函数y = ax(a≠0)的图象与反比例函致![]() (k≠0)的图象的一个
(k≠0)的图象的一个
交点为A(-1,2-k2),另—个交点为B,且A、B关于原点O对称,D为OB的中点,过点D的线段OB的垂直平分线与x轴、y轴分别交于C、E.
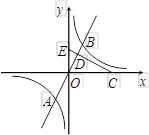
(1)写出反比例函数和正比例函数的解析式;
(2)试计算△COE的面积是△ODE面积的多少倍.
查看习题详情和答案>>
(本题满分10分)如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE、CD相交于点B.

(1)求证:直线AB是⊙O的切线.
(2)当AC=1,BE=2时,求tan∠OAC的值. 查看习题详情和答案>>

(1)求证:直线AB是⊙O的切线.
(2)当AC=1,BE=2时,求tan∠OAC的值. 查看习题详情和答案>>

 的图像与
的图像与 轴,
轴, 轴分别交于A(1,0)、B(0,-1)两点,且又与反比例函数
轴分别交于A(1,0)、B(0,-1)两点,且又与反比例函数 的图像在第一象限交于C点,C点的横坐标为2.
的图像在第一象限交于C点,C点的横坐标为2.