摘要： 如图.已知△ABC为直角三角形.∠ACB＝90°.AC＝BC.点A.C在x轴上.点B坐标为.线段AB与y轴相交于点D.以P(1.0)为顶点的二次函数图像经过点B.D． (1)请直接写出用m表示点A.D的坐标, (2)求这个二次函数的解析式, (3)点Q为二次函数图像上点P至点B之间的一点.连结PQ.BQ.求四边形ABQP面积的最大值．
网址：http://m.1010jiajiao.com/timu3_id_492700[举报]
（本小题满分10分）
如图，已知点E在直角△ABC的斜边AB上，以AE为直径的⊙O与直角边BC相切于点D，∠B = 30°．
求证：1.（1）AD平分∠BAC，2.（2）若BD = 
，求B E的长．
查看习题详情和答案>>
（本小题满分10分）
学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化.
类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）.如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义，解下列问题：
（1）sad 
的值为（ ）A. 
B.1 C. 
D.2
（2）对于
，∠A的正对值sad A的取值范围是 .
（3）已知
，其中
为锐角，试求sad的值.
查看习题详情和答案>>
（本小题满分10分）
如图，已知点E在直角△ABC的斜边AB上，以AE为直径的⊙O与直角边BC相切于点D，∠B = 30°．
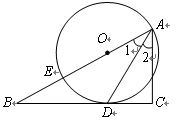
求证：【小题1】（1）AD平分∠BAC，【小题2】（2）若BD =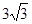
，求B E的长．
查看习题详情和答案>>
如图，已知点E在直角△ABC的斜边AB上，以AE为直径的⊙O与直角边BC相切于点D，∠B = 30°．
求证：【小题1】（1）AD平分∠BAC，【小题2】（2）若BD =
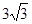，求B E的长．
查看习题详情和答案>>
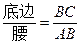.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.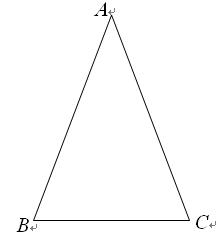
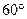的值为（ ）
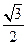
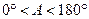，∠A的正对值sad A的取值范围是 .
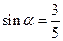，其中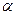
为锐角，试求sad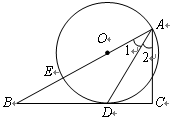
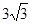，求B E的长．