摘要：二次函数与一元二次不等式的关系: 如图1, ①方程ax2+bx+c＝0的解是 , ②当x满足 时.函数值大于0, ③当x满足 时.函数值小于0. 如图2, ①方程ax2+bx+c＝0的解是 , ②当x满足 时.函数值大于0, ③当x满足 时.函数值小于0. [例题解析] 例1.已知抛物线y1＝2x2-8x+k+8和直线y2＝mx+1相交于点P. (1) 求这两个函数的关系式, (2) 求抛物线与直线的另一交点坐标. 解:在直线y2＝mx+1上. ∴有4m＝3m+1. 解得m＝1 ∴y1＝x+1.P(3.4). ∵点P(3.4)在抛物线y1＝2x2-8x+k+8上. ∴4＝18-24+k+8. 解得 k＝2 ∴y1＝2x2-8x+10. (2)依题意.得 解这个方程组.得. ∴抛物线与直线的另一交点坐标是. [实弹射击]
网址：http://m.1010jiajiao.com/timu3_id_491115[举报]
运用二次函数的性质和二次函数与一元二次方程的关系．画出函数
的草图，并根据草图(如图所示)，回答下列问题：
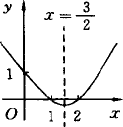
(1)当x取何值时，y小于零？当x取何值时，y大于零？
(2)能否用含x的不等式来描述(1)中的问题？
已知关于x的一元二次方程x2-4x+2（k-1）=0有两个不相等的实数根．
（1）求k的取值范围；
（2）如果抛物线y=x2-4x+2（k-1）与x轴的两个交点的横坐标为整数，求正整数k的值；
（3）直线y=x与（2）中的抛物线在第一象限内的交点为点C，点P是射线OC上的一个动点（点P不与点O、点C重合），过点P作垂直于x轴的直线，交抛物线于点M，点Q在直线PC上，距离点P为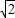
个单位长度，设点P的横坐标为t，△PMQ的面积为S，求出S与t之间的函数关系式．
查看习题详情和答案>>
（1）求k的取值范围；
（2）如果抛物线y=x2-4x+2（k-1）与x轴的两个交点的横坐标为整数，求正整数k的值；
（3）直线y=x与（2）中的抛物线在第一象限内的交点为点C，点P是射线OC上的一个动点（点P不与点O、点C重合），过点P作垂直于x轴的直线，交抛物线于点M，点Q在直线PC上，距离点P为
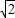个单位长度，设点P的横坐标为t，△PMQ的面积为S，求出S与t之间的函数关系式．
查看习题详情和答案>>
已知关于x的一元二次方程x2-4x+2（k-1）=0有两个不相等的实数根．
个单位长度，设点P的横坐标为t，△PMQ的面积为S，求出S与t之间的函数关系式．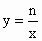
的图象的交点，且a，b是关于x的一元二次方程
的两个不相等的实数根，其中k为非负整数，m，n为常数．
（2012•丰台区二模）已知关于x的一元二次方程x2-4x+2（k-1）=0有两个不相等的实数根．