摘要： (1){3.1}+{1.2}={4.3}．----1分 (2)①画图 ----2分 最后的位置仍是B． ----3分 ②由①知.A ∴OC=AB==.OA=BC==. ∴四边形OABC是平行四边形． ----4分 (3){2.3}+{3.2}+{-5.-5}={0, 0}． ----5分
网址：http://m.1010jiajiao.com/timu3_id_489538[举报]
．画图题：（本题满分8分）
1.（1）在右面的三角形中（可以使用刻度尺、量角器、三角尺）
①画线段BC的中点D, 并连接AD；
②过点A画BC的垂线, 垂足为E；
③过点E画AB的平行线, 交AC于点F；
④指出图中表示点A到BC的距离的线段是： .
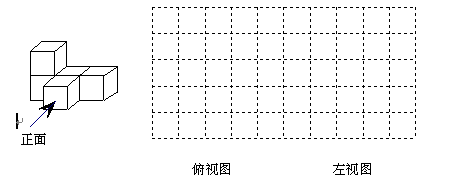
2.（2）①由大小相同的小立方块搭成的几何体如左图，请在右图的方格中画出该几何体的俯视图和左视图。
②用小立方体搭一几何体，使得它的俯视图和左视图与你在右图方格中所画的图一致，
则这样的几何体最少要_______个小立方块，最多要_______个小立方块。
查看习题详情和答案>>
（本题满分8分）我们知道当人的视线与物体表面互相垂直时的视觉效果最佳．如图是小明站在距离墙壁1.60米处观察装饰画时的示意图，此时小明的眼睛与装饰画底部A处于同一水平线上，视线恰好落在装饰画中心位置E处，且与AD垂直.已知装饰画的高度AD为0.66米，
求：⑴ 装饰画与墙壁的夹角∠CAD的度数（精确到1°）；
⑵ 装饰画顶部到墙壁的距离DC（精确到0.01米）.
查看习题详情和答案>>
（本题满分12分）
问题情境
已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？
数学模型
设该矩形的长为x，周长为y，则y与x的函数关系式为
．
探索研究
⑴我们可以借鉴以前研究函数的经验，先探索函数
的图象性质．
① 填写下表，画出函数的图象：
②观察图象，写出该函数两条不同类型的性质；
③在求二次函数y=ax2＋bx＋c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数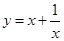
(x＞0)的最小值．
解决问题
⑵用上述方法解决“问题情境”中的问题，直接写出答案．
查看习题详情和答案>>
问题情境
已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？
数学模型
设该矩形的长为x，周长为y，则y与x的函数关系式为
．探索研究
⑴我们可以借鉴以前研究函数的经验，先探索函数
的图象性质．① 填写下表，画出函数的图象：
| x | … |  |  |  | 1 | 2 | 3 | 4 | … |
| y | … | | | | | | | | … |
③在求二次函数y=ax2＋bx＋c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数
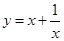(x＞0)的最小值．解决问题
⑵用上述方法解决“问题情境”中的问题，直接写出答案．
查看习题详情和答案>>
BC的距离的线段是： .
