摘要：20．已知每个网格中小正方形的边长都是1.图1 中的阴影图案是由三段以格点为圆心.半径分别为1和2的圆弧围成． (1)填空:图1中阴影部分的面积是 (结果保留), (2)请你在图2中以图1为基本图案.借助轴对称.平移或旋转设计 一个完整的花边图案(要求至少含有两种图形变换)．
网址：http://m.1010jiajiao.com/timu3_id_489295[举报]
“构造法”是一种重要方法，它没有固定的模式．要想用好它，需要有敏锐的观察、丰富的想象、灵活的构思．应用构造法解题的关键有二：一是要有明确的方向，即为什么目的而构造；二是要弄清条件的本质特点，以便重新进行组合．
例：在△ABC中，AB、BC、AC三边长分别是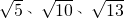
，求这个三角形的面积．
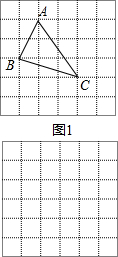
小辉在解这道题时，画一个正方形网格（每个正方形的边长为1），再在网格中画出格点（即的顶点都在小正方形的顶点处），如图1所示，这样不需要求的高，借助网格就能计算出它的面积．图中的面积，可以看成是一个的正方形的面积减去三个小三角形的面积：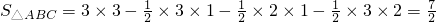
思维拓展：已知△ABC的边长分别为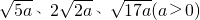
，请在下图所示的正方形网格中（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．
查看习题详情和答案>>
“构造法”是一种重要方法，它没有固定的模式．要想用好它，需要有敏锐的观察、丰富的想象、灵活的构思．应用构造法解题的关键有二：一是要有明确的方向，即为什么目的而构造；二是要弄清条件的本质特点，以便重新进行组合．
例：在△ABC中，AB、BC、AC三边长分别是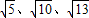
，求这个三角形的面积．
小辉在解这道题时，画一个正方形网格（每个正方形的边长为1），再在网格中画出格点（即的顶点都在小正方形的顶点处），如图1所示，这样不需要求的高，借助网格就能计算出它的面积．图中的面积，可以看成是一个的正方形的面积减去三个小三角形的面积：
思维拓展：已知△ABC的边长分别为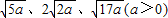
，请在下图所示的正方形网格中（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．
查看习题详情和答案>>
例：在△ABC中，AB、BC、AC三边长分别是
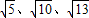，求这个三角形的面积．小辉在解这道题时，画一个正方形网格（每个正方形的边长为1），再在网格中画出格点（即的顶点都在小正方形的顶点处），如图1所示，这样不需要求的高，借助网格就能计算出它的面积．图中的面积，可以看成是一个的正方形的面积减去三个小三角形的面积：
思维拓展：已知△ABC的边长分别为
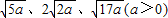，请在下图所示的正方形网格中（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．
查看习题详情和答案>>
“构造法”是一种重要方法，它没有固定的模式．要想用好它，需要有敏锐的观察、丰富的想象、灵活的构思．应用构造法解题的关键有二：一是要有明确的方向，即为什么目的而构造；二是要弄清条件的本质特点，以便重新进行组合．
例：在△ABC中，AB、BC、AC三边长分别是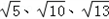
，求这个三角形的面积．小辉在解这道题时，画一个正方形网格（每个正方形的边长为1），再在网格中画出格点（即三角形的顶点都在小正方形的顶点处），
如图1所示，这样不需要求的高，借助网格就能计算出它的面积．图中的面积，可以看成是一个的正方形的面积减去三个小三角形的面积：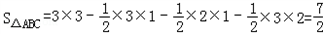
思维拓展：已知△ABC的边长分别为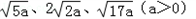
，请在下图所示的正方形网格中（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．
例：在△ABC中，AB、BC、AC三边长分别是
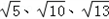，求这个三角形的面积．小辉在解这道题时，画一个正方形网格（每个正方形的边长为1），再在网格中画出格点（即三角形的顶点都在小正方形的顶点处），如图1所示，这样不需要求的高，借助网格就能计算出它的面积．图中的面积，可以看成是一个的正方形的面积减去三个小三角形的面积：
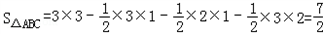
思维拓展：已知△ABC的边长分别为
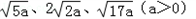，请在下图所示的正方形网格中（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．
“构造法”是一种重要方法，它没有固定的模式．要想用好它，需要有敏锐的观察、丰富的想象、灵活的构思．应用构造法解题的关键有二：一是要有明确的方向，即为什么目的而构造；二是要弄清条件的本质特点，以便重新进行组合．例：在△ABC中，AB、BC、AC三边长分别是
| 5 |
| 10 |
| 13 |
小辉在解这道题时，画一个正方形网格（每个正方形的边长为1），再在网格中画出格点（即的顶点都在小正方形的顶点处），如图1所示，这样不需要求的高，借助网格就能计算出它的面积．图中的面积，可以看成是一个的正方形的面积减去三个小三角形的面积：S△ABC=3×3-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
思维拓展：已知△ABC的边长分别为
| 5a |
| 2a |
| 17a |