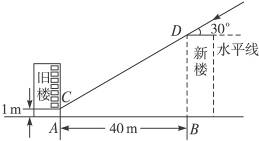
摘要:为解决楼房之间的挡光问题.某地区规定:两幢楼房间的距离至少为40 m.中午12时不能挡光.如图9-59.某旧楼的一楼窗台高1 m.要在此楼正南方40 m处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射.并且光线与水平线的夹角最小为30°.在不违反规定的情况下.请问新建楼房最高多少米?(结果精确到1 m.≈1.732.≈1.414) 图9-59 解:过点C作CE⊥BD于E.∵AB=40 m, ∴CE=40 m. ∵阳光入射角为30°, ∴∠DCE=30°. 在Rt△DCE中,tan∠DCE=, ∴=. ∴DE=40×≈23.而AC=BE=1 m, ∴DB=BE+ED=1+23=24(m). 答:新建楼房最高约24 m. 提示:将BD的长度转化成DE与BE的和.在△CED中.利用三角函数求出DE的长度.从而求解.
网址:http://m.1010jiajiao.com/timu3_id_489093[举报]
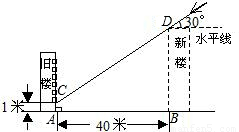
为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再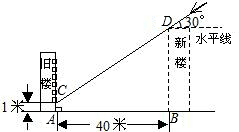 建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?
查看习题详情和答案>>
建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?
查看习题详情和答案>>
 建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?
查看习题详情和答案>>
建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?
查看习题详情和答案>>
为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再 建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?
建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?
查看习题详情和答案>>
为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再
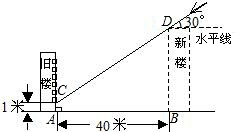
建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?
查看习题详情和答案>>

建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?