题目内容
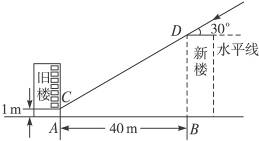
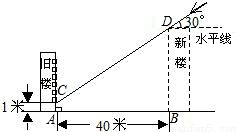
为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再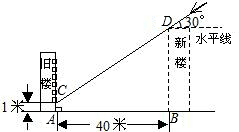 建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?
建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?
分析:在不违反规定的情况下,需使阳光能照到旧楼的一楼;据此构造Rt△DCE,其中有CE=30米,∠DCE=30°,解三角形可得DE的高度,再由DB=BE+ED可计算出新建楼房的最高高度.
解答: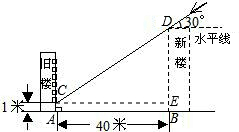 解:过点C作CE⊥BD于E.
解:过点C作CE⊥BD于E.
∵AB=40米,
∴CE=40米,
∵阳光入射角为30°,
∴∠DCE=30°,
在Rt△DCE中tan∠DCE=
.
∴
=
,
∴DE=40×
=
米,
∵AC=BE=1米,
∴DB=BE+ED=1+
=
米.
答:新建楼房最高为
米.
 解:过点C作CE⊥BD于E.
解:过点C作CE⊥BD于E.∵AB=40米,
∴CE=40米,
∵阳光入射角为30°,
∴∠DCE=30°,
在Rt△DCE中tan∠DCE=
| DE |
| CE |
∴
| DE |
| 40 |
| ||
| 3 |
∴DE=40×
| ||
| 3 |
40
| ||
| 3 |
∵AC=BE=1米,
∴DB=BE+ED=1+
40
| ||
| 3 |
3+40
| ||
| 3 |
答:新建楼房最高为
3+40
| ||
| 3 |
点评:本题考查了平行投影特点:在同一时刻,不同物体的物高和影长成比例.需注意通过投影的知识结合图形相似的性质巧妙地求解或解直角三角形.

练习册系列答案
相关题目
 建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?
建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?