摘要:如图.已知AB是⊙O的直径.点C在⊙O上.P是△OAC的重心.且OP=.∠A=30º. (1)求劣弧的长, (2)若∠ABD=120º.BD=1.求证:CD是⊙O的切线. 答案:.(1)解:延长OP交AC于E. ∵ P是△OAC的重心.OP=. ∴ OE=1. 且 E是AC的中点. ∵ OA=OC.∴ OE⊥AC. 在Rt△OAE中.∵ ∠A=30°.OE=1. ∴ OA=2. ∴ ∠AOE=60°. ∴ ∠AOC=120°. ∴ ︵AC=π. (2)证明:连结BC. ∵ E.O分别是线段AC.AB的中点. ∴ BC∥OE.且BC=2OE=2=OB=OC. ∴ △OBC是等边三角形. 法1:∴ ∠OBC=60°. ∵ ∠OBD=120°.∴ ∠CBD=60°=∠AOE. ∵ BD=1=OE.BC=OA. ∴ △OAE ≌△BCD. ∴ ∠BCD=30°. ∵ ∠OCB=60°. ∴ ∠OCD=90°. ∴ CD是⊙O的切线. 法2:过B作BF∥DC交CO于F. ∵ ∠BOC=60°.∠ABD=120°, ∴ OC∥BD. ∴ 四边形BDCF是平行四边形. ∴ CF=BD=1. ∵ OC=2. ∴ F是OC的中点. ∴ BF⊥OC. ∴ CD⊥OC. ∴ CD是⊙O的切线.
网址:http://m.1010jiajiao.com/timu3_id_489035[举报]
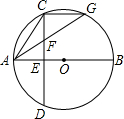 如图,已知AB是⊙O的直径,弦CD⊥AB于E,F是CE上的一点,且FC=FA,延长AF交⊙O于G,连接CG.
如图,已知AB是⊙O的直径,弦CD⊥AB于E,F是CE上的一点,且FC=FA,延长AF交⊙O于G,连接CG.(1)试判断△ACG的形状(按边分类),并证明你的结论;
(2)若⊙O的半径为5,OE=2,求CF•CD之值. 查看习题详情和答案>>
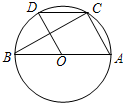 如图,已知AB是⊙O的直径,BC为弦,∠ABC=30°.过圆心O作OD⊥BC交弧BC于点D,连接DC,求∠DCB的度数.
如图,已知AB是⊙O的直径,BC为弦,∠ABC=30°.过圆心O作OD⊥BC交弧BC于点D,连接DC,求∠DCB的度数. (2013•淮北模拟)如图,已知AB是⊙O的直径,点C、D在⊙O上,且AB=10,AC=8.
(2013•淮北模拟)如图,已知AB是⊙O的直径,点C、D在⊙O上,且AB=10,AC=8.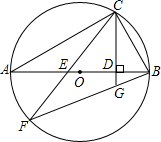 如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连接BF,与直线CD交于点G.求证:BC2=BG•BF.
如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连接BF,与直线CD交于点G.求证:BC2=BG•BF. 如图,已知AB是⊙O的直径,C是AB延长线上一点,BC=OB,CE是⊙O的切线,切点为D,过点A作AE⊥CE,垂足为E,则CD:DE的值是( )
如图,已知AB是⊙O的直径,C是AB延长线上一点,BC=OB,CE是⊙O的切线,切点为D,过点A作AE⊥CE,垂足为E,则CD:DE的值是( )