摘要：(2010年广西桂林适应训练).以RtΔABC的直角边AB为直径作圆O.与斜边交于点D,E为BC边上的中点.连接DE. (1)求证:DE是⊙O的切线, (2)连接OE.AE.当∠CAB为何值时.四边形AOED是平行四边形?并在此条件下求 sin∠CAE的值. 答案:(1)连接OD.BD ∵ΔBDC是RtΔ, 且E为BC中点. ∴∠EDB=∠EBD. 又∵OD=OB 且∠EBD+∠DBO=90° ∴∠EDB+∠ODB=90° ∴DE是⊙O的切线, (2)∵∠EDO=∠B=90°, 若要AOED是平行四边形.则DE∥AB,D为AC中点. 又∵BD⊥AC, ∴ΔABC为等腰直角三角形. ∴∠CAB=45°. 过E作EH⊥AC于H. 设BC=2k. 则EH= ∴sin∠CAE=
网址：http://m.1010jiajiao.com/timu3_id_489029[举报]
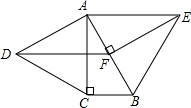如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE．若∠BAC=30°，EF⊥AB，垂足为F，连结DF．求证：（1）△ABC≌△EAF；
（2）四边形ADFE是平行四边形．
已知：如图，以Rt△ABC的直角边AC为直径作⊙O，交AB于D点，OE∥AB交BC于E点，求证：DE为⊙O的切线．
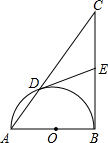如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D．（1）若点E是BC边上的中点，连接DE．证明：DE与半圆O相切；
（2）请你写出（1）的逆命题，并判断是否成立．为什么？
（3）若AC、AB的长是方程x2-10x+24=0的两个根，求直角边BC的长．
（2009•黔南州）如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连接DE．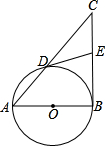
如图，以Rt△ABC的直角边AB为直径作圆O与斜边AC交于点D，E为BC边的中点，连接DE．