摘要:(2010年 湖里区 二次适应性考试)如图.四边形ABCD内接于⊙O.BD是⊙O的直径. AE⊥CD于点E.DA平分∠BDE. (1)求证:AE是⊙O的切线.(2)若∠DBC=30°.DE=1 cm.求BD的长. 答案: (1)证明:连结OA ∵AD平分∠BDE ∴∠ADE=∠ADO ∵OA=OD ∴∠OAD=∠ADO ∴∠ADE=∠OAD ∴OA∥CE ∵AE⊥CD ∴AE⊥OA ∴AE是⊙O的切线 (2)∵BD是⊙O的直径 ∴∠BCD=90° ∵∠DBC=30° ∴∠BDE=120° ∵AD平分∠BDE ∴∠ADE=∠ADO=60° ∵OA=OD ∴△OAD是等边三角形 ∴AD=OD=BD 在Rt△AED中.DE=1.∠ADE=60° ∴AD= = 2 ∴BD=4
网址:http://m.1010jiajiao.com/timu3_id_489025[举报]
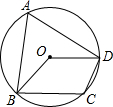 如图,四边形ABCD内接于⊙O,∠BOD=110°,则∠BCD=
如图,四边形ABCD内接于⊙O,∠BOD=110°,则∠BCD=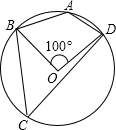 如图,四边形ABCD内接于⊙O,若∠BOD=100°,则∠DAB的度数为( )
如图,四边形ABCD内接于⊙O,若∠BOD=100°,则∠DAB的度数为( )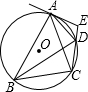 已知:如图,四边形ABCD内接于⊙O,过点A的切线与CD的延长线交于E,且∠ADE=∠BDC.
已知:如图,四边形ABCD内接于⊙O,过点A的切线与CD的延长线交于E,且∠ADE=∠BDC.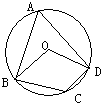 17、如图,四边形ABCD内接于⊙O,若∠BCD=130°,则∠BOD=
17、如图,四边形ABCD内接于⊙O,若∠BCD=130°,则∠BOD=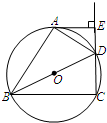 25、如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD,垂足为E,DA平分∠BDE.
25、如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD,垂足为E,DA平分∠BDE.