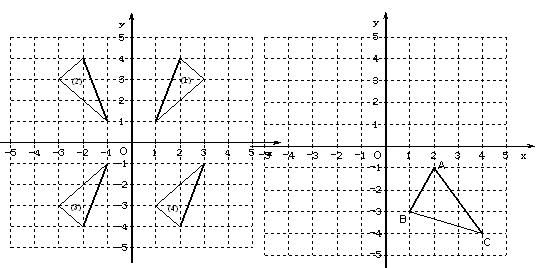
摘要：下面左图所示的几何体的俯视图是( ) 答案:D
网址：http://m.1010jiajiao.com/timu3_id_488968[举报]
国际数学家大会的会标如下面左图所示，它取材于我国三国时期（公元3世纪）赵爽所著的《勾股圆方图注》．把这个图案沿图中线段剪开后，能拼成如右图所示的四个图形，则其中是轴对称图形的有（ ）
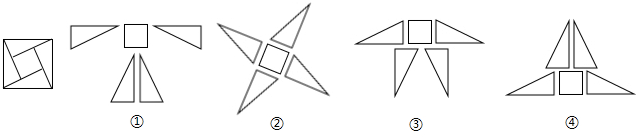
查看习题详情和答案>>
请大家阅读下面两段材料，并解答问题：
材料1：我们知道在数轴上表示4和1的两点之间的距离为3，（如图）而|4-1|=3，所以在数轴上表示4和1的两点之间的距离为|4-1|．
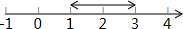
再如在数轴上表示4和-2的两点之间的距离为6，（如图）
而|4-（-2）|=6，所以数轴上表示数4和-2的两点之间的距离为|4-（-2）|．
根据上述规律，我们可以得出结论：在数轴上表示数a和数b两点之间的距离等于|a-b|（如图）
材料2：如下左图所示大正方形的边长为a，小正方形的边长为b，则阴影部分的面积可表示为：a2-b2．
将上图中的左图重新拼接成右图，则阴影部分的面积可表示为（a+b）（a-b），由此可以得到等式：a2-b2=（a+b）（a-b），
阅读后思考：
（1）试一试，求在数轴上表示的数5
与-4
的两点之间的距离为 ；
（2）请用材料2公式计算：（49
）2-（49
）2= ；
（3）上述两段材料中，主要体现了数学中 的数学思想．
查看习题详情和答案>>
材料1：我们知道在数轴上表示4和1的两点之间的距离为3，（如图）而|4-1|=3，所以在数轴上表示4和1的两点之间的距离为|4-1|．
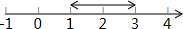
再如在数轴上表示4和-2的两点之间的距离为6，（如图）
而|4-（-2）|=6，所以数轴上表示数4和-2的两点之间的距离为|4-（-2）|．
根据上述规律，我们可以得出结论：在数轴上表示数a和数b两点之间的距离等于|a-b|（如图）
材料2：如下左图所示大正方形的边长为a，小正方形的边长为b，则阴影部分的面积可表示为：a2-b2．
将上图中的左图重新拼接成右图，则阴影部分的面积可表示为（a+b）（a-b），由此可以得到等式：a2-b2=（a+b）（a-b），
阅读后思考：
（1）试一试，求在数轴上表示的数5
| 2 |
| 3 |
| 1 |
| 4 |
（2）请用材料2公式计算：（49
| 8 |
| 9 |
| 1 |
| 9 |
（3）上述两段材料中，主要体现了数学中
请大家阅读下面两段材料，并解答问题：材料1：我们知道在数轴上表示4和1的两点之间的距离为3，（如图）而|4﹣1|=3，所以在数轴上表示4和1的两点之间的距离为|4﹣1|．
再如在数轴上表示4和﹣2的两点之间的距离为6，（如图）
而|4﹣（﹣2）|=6，所以数轴上表示数4和﹣2的两点之间的距离为|4﹣（﹣2）|．根据上述规律，我们可以得出结论：在数轴上表示数a和数b两点之间的距离等于|a﹣b|（如图）
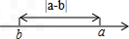
材料2：如下左图所示大正方形的边长为a，小正方形的边长为b，则阴影部分的面积可表示为：a2﹣b2．
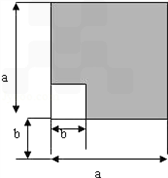
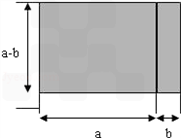
将上图中的左图重新拼接成右图，则阴影部分的面积可表示为（a+b）（a﹣b），由此可以得到等式：a2﹣b2=（a+b）（a﹣b），阅读后思考：
（1）试一试，求在数轴上表示的数
与
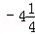的两点之间的距离为（ ）；
（2）请用材料2公式计算：（49
）2﹣（49
）2=（ ）；
（3）上述两段材料中，主要体现了数学中（ ）.
查看习题详情和答案>>
（1）试一试，求在数轴上表示的数
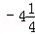与的两点之间的距离为（ ）；（2）请用材料2公式计算：（49
）2﹣（49）2=（ ）；（3）上述两段材料中，主要体现了数学中（ ）.
