摘要：已知.在Rt△ABC中.∠C=90°.∠A=30°.CD是AB边的中线.若将△ABC沿CD折叠.使CA到的位置.连结B． (1)求证:四边形是菱形, (2)若BC＝2.试求四边形是菱形的面积. (1) ∵∠ACB=90°,∠A=30°． ∴BC=AB. 又CD是斜边AB的中线. ∴CD=AD=AB =BD． ∴BC =AD= CD =BD, ∴30°. ∵将△ABC沿CD折叠得△. ∴,30°. ∴60°-30°=30°. ∴∥CB. ∴四边形为菱形. (2)∵BC=2.∴BD=2.易得.∴S=2.
网址：http://m.1010jiajiao.com/timu3_id_488220[举报]
已知：在Rt△ABC中，∠B=90°，BC=4cm，AB=8cm，D、E、F分别为AB、AC、BC边上的中点．若P为AB边上的一个动点，PQ∥BC，且交AC于点Q，以PQ为一边，在点A的异侧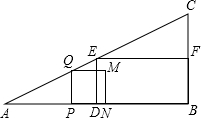
作正方形PQMN，记正方形PQMN与矩形EDBF的公共部分的面积为y．
（1）如图，当AP=3cm时，求y的值；
（2）设AP=xcm，试用含x的代数式表示y（cm2）；
（3）当y=2cm2时，试确定点P的位置． 查看习题详情和答案>>
作正方形PQMN，记正方形PQMN与矩形EDBF的公共部分的面积为y．（1）如图，当AP=3cm时，求y的值；
（2）设AP=xcm，试用含x的代数式表示y（cm2）；
（3）当y=2cm2时，试确定点P的位置． 查看习题详情和答案>>
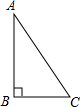已知，在Rt△ABC中，∠A=20°，则∠C的度数是（ ）
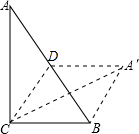已知，在Rt△ABC中，∠C=90°，∠A=30°，CD是AB边的中线，若将△ABC沿CD折叠，使CA到CA′的位置，连接A′B．